正規分布
公式
積率母関数 | eμt+2σ2t2 |
確率密度関数 | f(x)=2πσ21exp[−2σ2(x−μ)2] |
期待値 | E(X)=μ |
分散 | V(X)=σ2 |
グラフの形
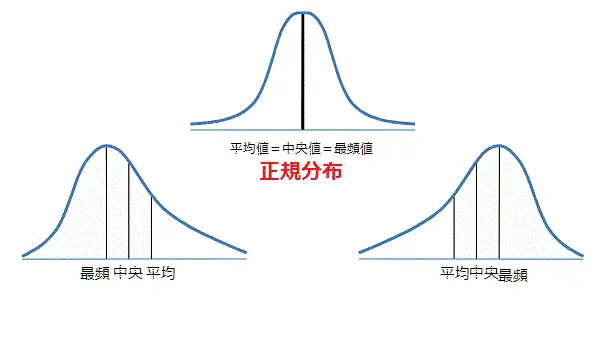
関連記事
正規分布の公式と特徴まとめ
確率密度関数を用いた正規分布の期待値(平均)と分散の導出
積率母関数を用いた正規分布の期待値(平均)と分散の導出
連続一様分布
公式
積率母関数 | t(b−a)etb−eta |
確率密度関数 | f(x)={b−a10(a≤x≤b)(otherwise) |
期待値 | E(X)=21(a+b) |
分散 | V(X)=121(b−a)2 |
グラフの形
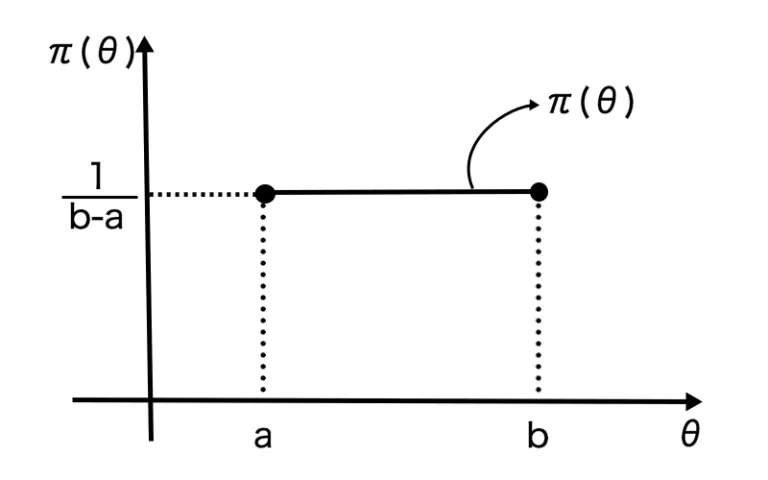
関連記事
積率母関数を用いた連続一様分布の期待値(平均)と分散の導出
確率密度関数を用いた連続一様分布の期待値(平均)と分散の導出
指数分布
公式
積率母関数 | MX(t)=λ−tλ |
確率密度関数 | f(X;λ)=λe−λx |
期待値 | E(X)=λ1 |
分散 | V(X)=λ21 |
関連記事
指数分布とは
積率母関数を用いた指数分布の期待値・分散の導出
確率密度関数を用いた指数分布の期待値・分散の導出
ガンマ分布
一言で説明
ガンマ分布は非負の連続確率分布であり、パラメータkとθを持ちます。
公式
積率母関数 | MX(t)=(1−θt1)k |
確率密度関数 | f(x)=Γ(k)θkxk−1e−θx |
期待値 | E(X)=kθ |
分散 | V(X)=kθ2 |
関連記事
ガンマ分布とは
積率母関数を用いたガンマ分布の期待値・分散の導出
確率密度関数を用いたガンマ分布の期待値・分散の導出
ベータ分布
一言で説明
ベータ分布は、αとβの2つのパラメータによって特徴づけられる分布です。
公式
確率密度関数 | f(x)=B(α,β)xα−1(1−x)β−1 |
期待値 | E(X)=α+βα |
分散 | V(X)=(α+β)2(α+β+1)αβ |
関連記事
ベータ分布とは?期待値と分散の導出も解説
ディリクレ分布
一言で説明
ディリクレ分布とは、ベータ分布を多変量に拡張した分布です。
公式
確率密度関数 | f(x1,x2,...,xn−1)=Γ(α1)...Γ(αn)Γ(∑i=1nαi)x1α1−1x2α2−1...xnαn−1 ただし、∑i=1nxi=1とし、x1,...,xn≥0とする。 |
期待値 | E(Xi)=∑i=1nαiαi (i=1,...,n−1) |
分散 | V(Xi)=(∑i=1nαi)2(∑i=1nαi+1)αi(∑i=1nαi−αi)(i=1,...,n−1) |
関連記事
ディリクレ分布とは?期待値・分散・共分散の導出も解説
カイ二乗分布
一言で説明
確率変数Z1,Z2,...,Znが互いに独立であり、それぞれが標準正規分布N(0,1)に従うとき、
χ2=Z12+Z22+,...,+Zk2
のχ2に従う分布を、自由度k(足される標準正規分布の数)のカイ二乗分布と言います。
公式
積率母関数 | MX(t)=(1−2t1)2k |
確率密度関数(自由度k) | f(x)=22kΓ(2k)x2k−1e−2x |
期待値 | E(x)=k |
分散 | V(x)=2k |
グラフの形
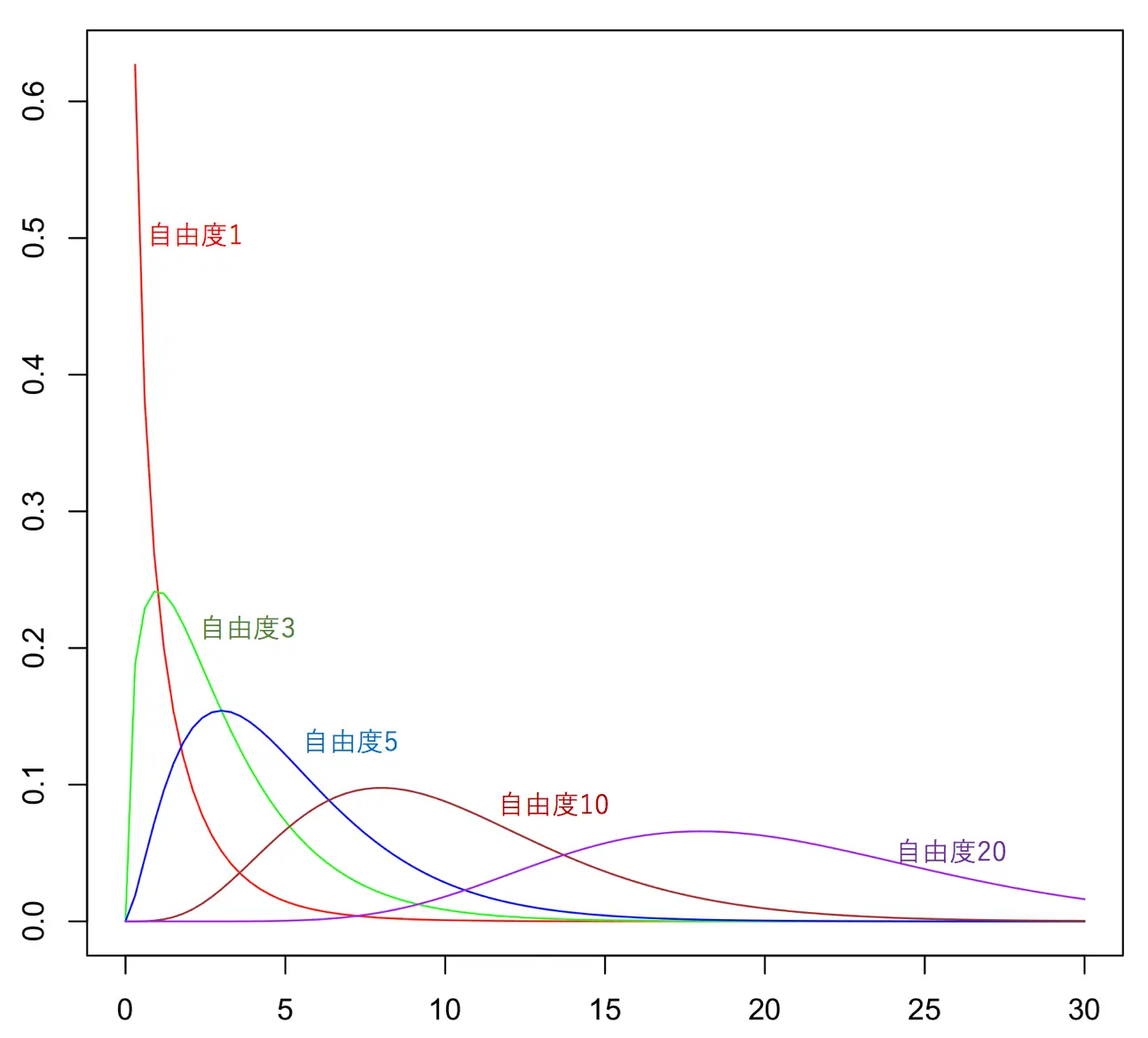
関連記事
カイ二乗分布のわかりやすいまとめ
積率母関数を用いたカイ二乗分布の期待値と分散の導出
確率密度関数を用いたカイ二乗分布の期待値と分散の導出
t分布
一言で説明
確率変数Zが標準正規分布N(0,1)、確率変数Wが自由度nのカイ二乗分布に従うとき、
t=nWZ
と表されるtが従う分布を、t分布といいます。
公式
確率密度関数 | f(x)=νπΓ(2ν)Γ(2ν+1)(1+νx2)−(2ν+1) |
期待値 | E(X)=0 |
分散 | V(X)={∞γ−2γ(1<γ≤2)(γ>2) |
グラフの形
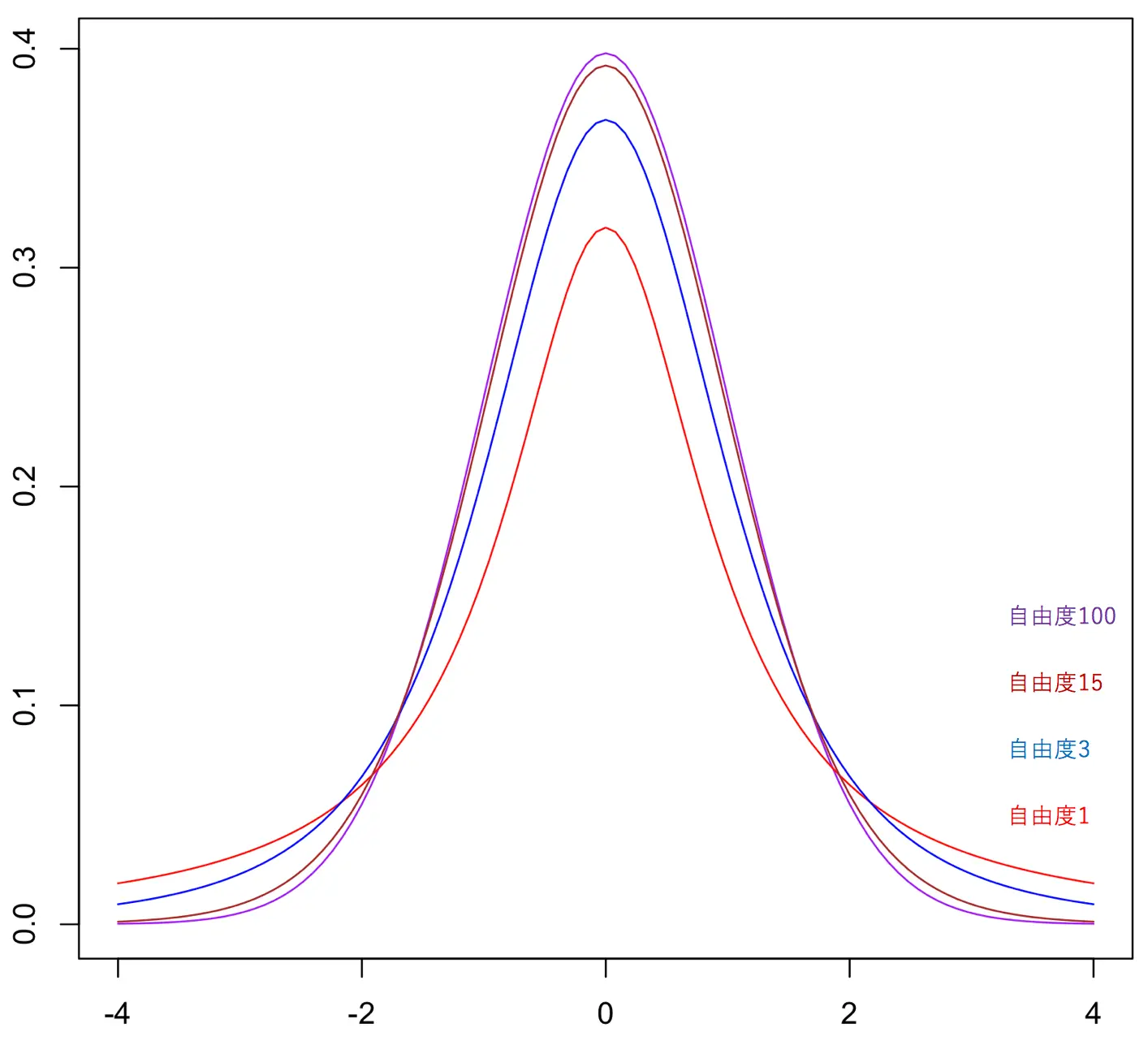
関連記事
t分布とは
片側t分布表と見方
確率密度関数を用いたt分布の期待値の導出
F分布
一言で説明
F分布とは、XとYが互いに独立である確率変数X,Yについて、Xが自由度nのカイ二乗分布、確率変数Yが自由度mのカイ二乗分布に従うとき、F=mYnXと表されるFが従う確率分布です。
グラフの形
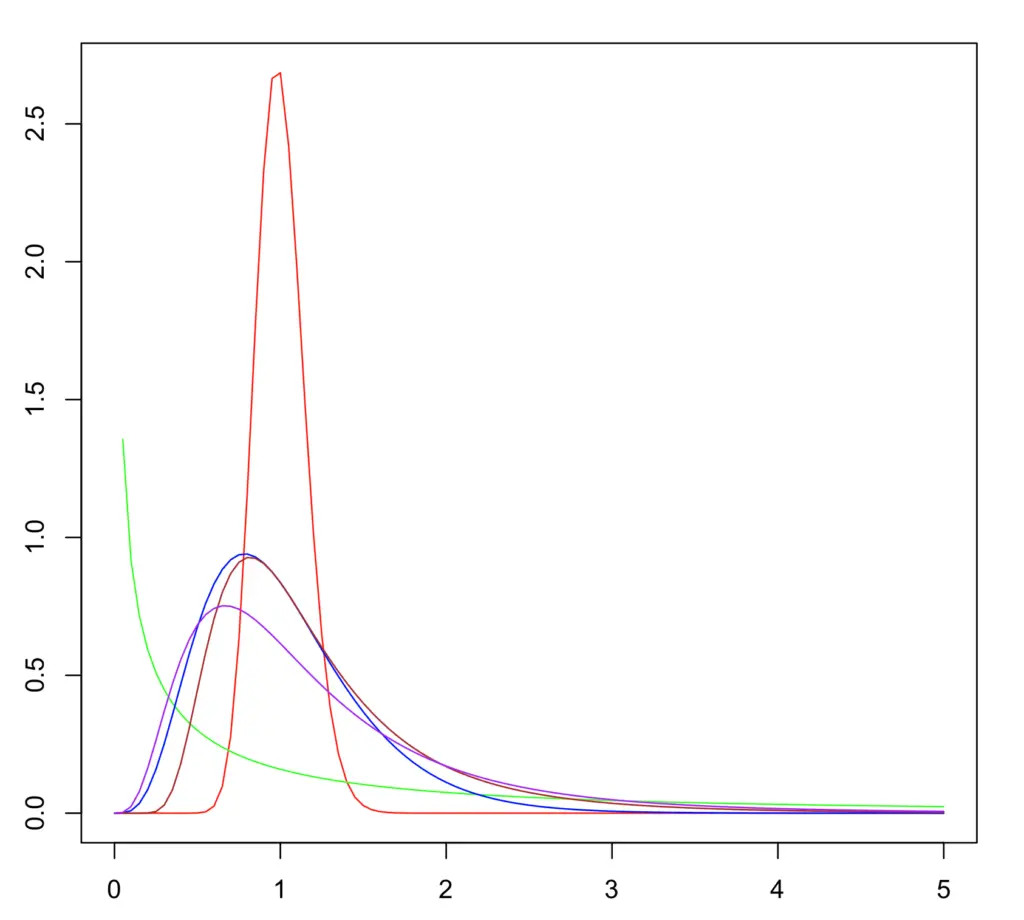
公式
確率密度関数 | f(z)=B(2n,2m)(mn)2n(1+mnz)−2n+mz2n−1 |
期待値 | E(Z)=m−2m |
分散 | V(Z)=n(m−2)2(m−4)2m2(n+m−2) |
関連記事
F分布とは
F分布の確率密度関数をカイ二乗分布を用いて導出
カイ二乗分布を用いたF分布の期待値と分散の導出
確率密度関数を用いたF分布の期待値と分散の導出
離散一様分布
公式
積率母関数 | MX(t)=Net1−et1−etN |
確率質量関数 | f(x)=N1 |
期待値 | E(X)=2N+1 |
分散 | V(X)=12N2−1 |
関連記事
積率母関数を用いた離散一様分布の期待値・分散の導出
確率質量関数を用いた離散一様分布の期待値・分散の導出
ベルヌーイ分布
一言で説明
ベルヌーイ分布とは、ベルヌーイ試行の結果を0と1で表した確率分布です。
公式
確率質量関数 | f(k;p)=pk(1−p)(1−k) |
期待値 | E(X)=p |
分散 | V(X)=p(1−p) |
関連記事
ベルヌーイ分布の分かりやすいまとめ
確率密度関数を用いたベルヌーイ分布の期待値(平均)と分散の導出
二項分布
一言で説明
二項分布とは、互いに独立した成功確率pベルヌーイ試行をn回行ったときに、ある事象が何回起こるかについての確率分布です。
公式
積率母関数 | MX(t)=(etp+1−p)n |
確率質量関数 | P(X=k)=(nk)pk(1−p)n−k |
期待値 | E(X)=np |
分散 | V(X)=np(1−p) |
関連記事
二項分布のわかりやすいまとめ
積率母関数を用いた二項分布の期待値・分散の導出
確率質量関数を用いた二項分布の期待値・分散の導出
確率質量関数を用いた二項分布の最頻値の導出
二項分布の歪度と尖度の導出
多項分布
一言で説明
多項分布とは、二項分布を一般化した確率分布です。
公式
確率密度関数 | f(x1,x2,...,xk)=x1!x2!...xk!n!p1x1 p2x2... pkxk (xi≥0,x1+...+xk=n) ただし、nは整数であり、pi>0(i=1,2,...,k),p1+p2+...+pk=1 |
期待値 | E(Xi)=npi (i=1,...,k) |
分散 | V(Xi)=npi(1−pi) (i=1,...,k) |
関連記事
多項分布とは?期待値・分散・共分散の導出も解説
ポアソン分布
一言で説明
ポアソン分布とは、二項分布B(n,p)において、期待値np=λを固定し、試行回数nと成功確率pをそれぞれn→∞、p→0としたときに得られる確率分布です。
公式
積率母関数 | MX(t)=eλ(et−1) |
確率質量関数 | P(X=k)=k!λke−λ |
期待値 | E(X)=λ |
分散 | V(X)=λ |
グラフの形
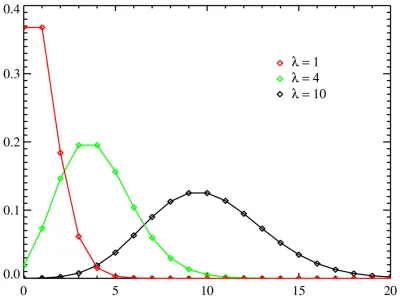
関連記事
積率母関数を用いたポアソン分布の期待値と分散の導出
確率質量関数を用いたポアソン分布の期待値と分散の導出
幾何分布
一言で説明
幾何分布とは、成功確率pのベルヌーイ試行を、初めて成功するまで繰り返した時の試行回数xの確率分布です。
公式
積率母関数 | 1−(1−p)etpet |
確率関数 | f(x)=p(1−p)x−1 ただし、x=1,2,⋯ |
期待値 | E[x]=p1 |
分散 | V[x]=p21−p |
関連記事
幾何分布とは?期待値と分散の導出も解説
超幾何分布
一言で説明
超幾何分布とは、以下のような事象があったとき、Xが従う確率分布です。
超幾何分布の例
箱の中にk個の赤いボール、N−k個の青いボール、計N個のボールがある。
箱の中からn個のボールを取り出したとき、その中に含まれる赤いボールの個数をX個とする。
公式
確率密度関数 | p(x)=⎩⎨⎧(Nn)(kx)(N−kn−x)0(x=0,1,2,⋯,n)(else) |
期待値 | E(X)=nNk |
分散 | V(X)=N2(N−1)nk(N−k)(N−n) |
関連記事
超幾何分布とは?期待値と分散の導出も解説
関連記事
期待値とは?定義や性質を解説
分散とは?2種類の公式と計算例を解説
積率母関数とは












