ベイズ統計学とは？初心者にもわかりやすく解説

ベイズ統計学とは

ベイズ統計学とは、ベイズの定理をもとにした統計的な考え方の一種です。

記述統計学・推計統計学とは異なる考え方をします。

ベイズ統計学が注目されている理由

ベイズ統計学の基になっているベイズの定理は1700年代から存在していました。古い歴史のあるこの領域が、今再注目されている理由を解説します。

ベイズ統計学の歴史

ベイズ統計学は、1700年中頃にトーマズベイズによる、ベイズの定理の発表により、産声をあげました。その後、1800年代後半に再び現在のベイズ統計の考え方の基礎となる考え方をする人々が現れました。

しかし、推計統計学論者のフィッシャーらが、「主観確率を扱うのは科学的でない」とし、ベイズ統計学は闇に葬り去られてしまったのです。

科学的であるかないかは別として、ベイズ統計学は現実に役に立つ学問であるということがが徐々に認められ、1950年代に入り再び研究され注目を浴びるようになりました。

機械学習とベイズ統計学の関係

機械学習とは、機械（コンピュータ）がデータからルールやパターンなどの法則性見つけ出し、その法則から将来を予測することです。
この機械学習にも、ベイズ統計が活用されています。

具体的に、迷惑メール判定の機械学習モデルには、ベイジアンフィルターと呼ばれるメールフィルターが採用されていることがあります。

事前に迷惑メールについての定義を作っておき、迷惑メールとして分別されたメール（または、ユーザーが迷惑メールフォルダーに移動したメール）から法則を見つけ、その法則を元に、新たに受信されるメールについて迷惑メール判定をします。

これにより、日々変化する迷惑メールに対応して、正しい判別をすることができるのです。

客観確率と主観確率

確率には、「客観確率」と「主観確率」があります。

客観確率とは、「サイコロで6の目が出る確率は1/6である」というような、誰もが同一の答えを導き出せるような確率です。

主観確率とは、「人によって答えが違う確率」です。
例えば、「電車で隣の席に座っている社会人が転職を考えている確率は？」という問いに対して、皆さんが主観的に「これくらいか？」と導き出した確率が主観確率です。

ベイズ統計学が使う確率は主観確率になります。

事前確率と事後確率

ベイズ統計学は、事前確率（prior probability）と事後確率(posterior probability)を用いて計算を進めていきます。

ここでも、「電車で隣の席に座っている社会人が転職を考えている確率」を例にとって考えてみます。

ステップ1：何も分からない状態

隣に座ってきたばかりの社会人が転職を考えているかどうか分からないので、仮に、転職を考えている確率（主観確率）を50%に設定します。
（通常、何も情報がない段階で設定する確率は1/2とすることが多いです）

事前確率：50%

ステップ2：社会人の行動を観察

社会人は、席の正面にある転職に関する広告をずっと眺めています。転職を考えている確率が高そうだと思い、確率を70％に上げます。

事前確率：50%
事後確率：70%

このように、「転職に関する広告を眺めている」という事象が分かった後に設定した確率を事後確率といい、その前に設定していた確率を事前確率といいます。
事前確率を設定した後に、何か新たな情報を取得し、事後確率を更新していくという操作を繰り返していく仕組みです。

以上から、ベイズ統計学の考え方には学習能力があると言えます。

ベイズの定理

事前確率を設定した後のアップデートは、ベイズの定理に基づいて行います。式は以下のようになります。

$P(A|X)=\frac{P(X|A)P(A)}{P(X)}= P(A)×\frac{P(X|A)}{P(X)}$

$P(A|X)$：事象$X$が起こった状況下で事象$A$が起こる確率（事後確率）
$P(A)$：事象$A$が起こる確率（事前確率）
$P(X)$：事象$X$が起こる確率
$P(X|A)$：事象$A$が起こった状況下で事象Xが起こる確率

数式を言葉で表現すると、以下のようになります。

$事後確率　=　事前確率　×　\frac{ある場合においての、そのデータが得られる確率}{そのデータが得られる確率}$

参考記事：ベイズの定理の導出

ベイズ推定の定義と性質

ベイズ統計には、点推定の一種としてベイズ推定量があります。

ベイズ推定の定義

ベイズ推定量の定義

平均リスク$r(\pi,\delta)$を最小にするような$\theta$の推定量$T=\delta(x_1,x_2,...,x_n)$があるとき、この$T$を事前分布$\pi(\theta)$に対するベイズ推定量という。

ベイズ推定には、決定理論という概念を使います。決定理論とは、得られた情報（データ）からどのような行動をとると決定するかを、数学・統計学的に行う理論のことです。

このベイズ推定量の定義とその考え方については「ベイズ推定の定義や考え方を解説」をご確認ください。

ベイズ推定の性質

ベイズ推定の性質

ベイズ推定量は、事後分布の平均と一致する

この性質を利用することにより、ベイズ推定量を定義からではなく、事後分布の平均から求めることができるようになります。

上記の性質については、以下のページをご確認ください。

ベイズ推定量の性質と導出を例題を用いて解説

正規分布の事後分布の平均と分散

ベルヌーイ分布の事後分布の平均と分散

ベイズ推定量と最尤推定量の違い

最尤推定とベイズ推定はよく比較されることがあります。最尤推定量は頻度論の考え方に基づいた推定であるのに対し、ベイズ推定はベイズ論に基づいた推定です。

この二つの推定量の違いは、最尤推定量は事前情報を使わないのに対し、ベイズ推定は事前情報を使うという点にあります。

共役事前分布とは

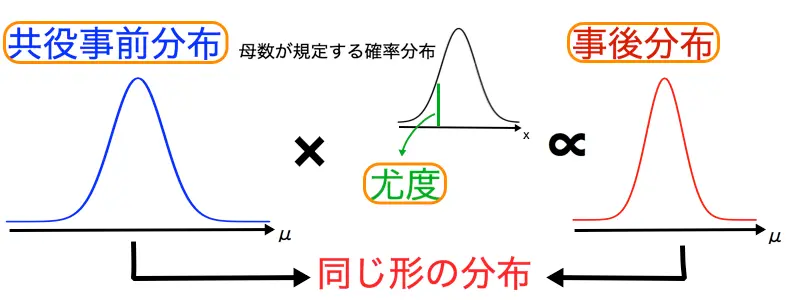
共役事前分布とは、ベイズ統計を扱う際に、複雑な計算を回避するために考えられた事前分布です。

共役事前分布を用いて事後分布を求めると、事後分布が事前分布と同じ分布になるという特性があります。

共役事前分布に関して「共役事前分布を分かりやすく解説」をご確認ください。

ベイズ流の仮説検定

全6回にわたってベイズ流の仮説検定について解説しています。

第1回：ベイズ統計と仮説検定【1】～頻度論との違い～

頻度論における仮説検定は$P(X|H_i)$を導出していたのに対し、ベイズ統計における仮説検定は$P(H_i|X)$を導出します。

よって、従来の仮説検定とは違ったアプローチで検定を行う必要があります。

第2回：ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～

$P(H_i|X)$はデータが与えられた上での仮説を満たす確率です。

つまり、ベイズ統計の仮説検定では仮説が成り立つ確率を直接計算できます。そこで、帰無仮説が成り立つ確率と、対立仮説が成り立つ確率を算出し、大きい確率である方の仮説を受容する、という検定問題を考えました。

第3回：ベイズ統計と仮説検定【3】～頻度論の考え方に基づくベイズ統計の仮説検定～

従来の仮説検定の考え方では、帰無仮説は安易に棄却してはいけないという考え方があります。そこで、その考え方を取り入れたベイズ流仮説検定を考えました。

従来の仮説検定の「第1種の過誤の確率を一定以下に抑える」という考え方に基づいて、事後オッズ比を一定以下に抑える検定問題を考えました。

第4回：ベイズ統計と仮説検定【4】～ベイズファクター～

事前確率を含めた事前分布は、自分で設定する必要があります。その設定の仕方によって、仮説の棄却されやすさに差が生じてしまいます。

そこで、ベイズファクターという指標を導入し、検定結果だけでなく、その検定の証拠の強さも評価することを考えました。

第5回：ベイズ統計と仮説検定【5】～点帰無仮説におけるベイズ流の仮説検定～

帰無仮説が点帰無仮説の場合、事前確率が0になってしまいます。そこで、事前確率を自分で割り当てた上で検定を行いました。

第6回：ベイズ統計と仮説検定【6】～ベイズ流仮説検定の問題点～

事前分布には非正則分布を使うことはできません。幅のある仮説を立てると、割り当てられる確率が無限になり、ベイズファクターに正当な解釈を与えないからです。

また、頻度論の検定に比べると、ベイズ流仮説検定は帰無仮説が棄却されにくい傾向にあります。

関連記事

ベイズの定理の導出

ベイズ推定の定義や考え方を解説

ベイズ推定量の性質と導出を例題を用いて解説

正規分布の事後分布の平均と分散

ベルヌーイ分布の事後分布の平均と分散