ベイズ統計と仮説検定4～ベイズファクター～

ベイズ統計における仮説検定の問題点

ベイズ統計における仮説検定には「事後オッズ比が事前分布の設定によって左右される」という問題があります。

事後分布が事前分布によって得られることはベイズの定理から証明することができます。

例えば、以下のような仮説検定を考えます。

$H_0:\theta\leq\theta_0$
$H_1:\theta\gt\theta_0$

また、事前分布を以下の図のように設定します。

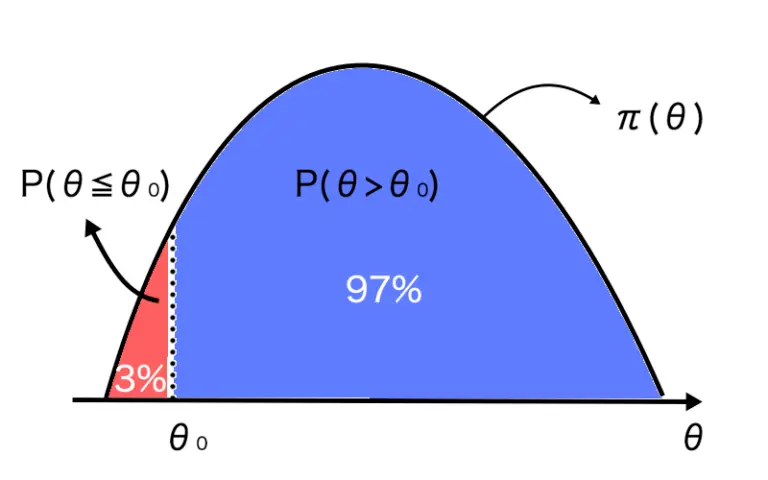
上記の分布だと、有意水準pが5%の場合、すでに帰無仮説が棄却されてしまう状態です。

このようにベイズ統計の仮説検定には、事前に設定する確率によって、帰無仮説を棄却する可能性に差が生じるという弱点があります。

ベイズファクターとは

上記のようなベイズ統計の仮説検定の弱点を補うために、ベイズファクターを使います。

ベイズファクターとは、仮説検定の証拠の強さを表します。

例えば、以下のような仮説検定を考えます。

$H_0:\theta\in\Theta_0$
$H_1:\theta\in\Theta_1$

$\pi_0$と$1-\pi_0$をそれぞれ$\Theta_0$と$\Theta_1$の事前確率とします。これを図で表すと、以下のようになります。

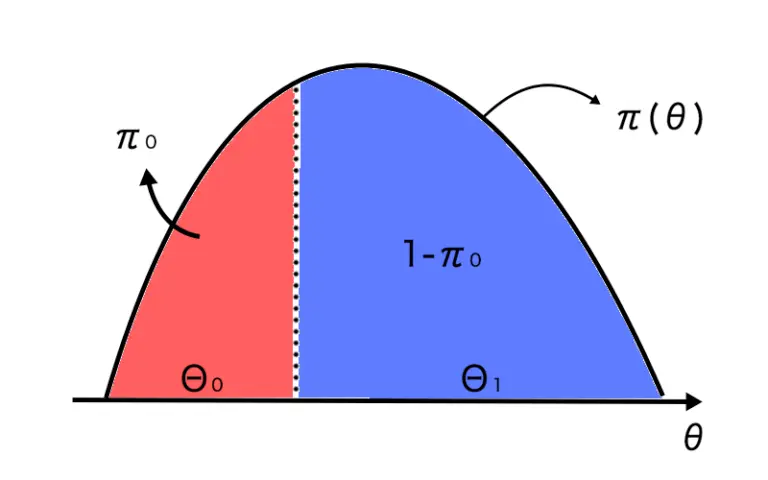
$g_i(\theta)$を$\Theta_i$のもとでの$\theta$の事前分布の密度関数とすると、

$g_i(\theta)=\frac{\pi(\theta)}{\int_{\theta\in\Theta_i}\pi(\theta)d\theta}$

であるから、

$g_0(\theta)=\frac{\pi(\theta)}{\int_{\theta\in\Theta_0}\pi(\theta)d\theta}=\frac{\pi(\theta)}{\pi_0}$
$g_1(\theta)=\frac{\pi(\theta)}{\int_{\theta\in\Theta_1}\pi(\theta)d\theta}=\frac{\pi(\theta)}{1-\pi_0}$

と与えられます。

よって、事前分布は以下のように分解することができます。

$\pi(\theta)=\pi_0g_0(\theta)I(\theta\in\Theta_0)+(1-\pi_0)g_1(\theta)I(\theta\in\Theta_1)$

$I(・)$は指示関数

これを利用して事後オッズ比を導出していきます。

事前分布$\pi(\theta)$のもとでのXの周辺尤度を$m_{\pi}(x)$とすると、事後分布$\pi(\theta|x)$はベイズの定理より、以下のように与えられます。

$\pi(\theta|x)=\frac{f(x|\theta)\pi(\theta)}{m_{\pi}(x)}$

この式は、$\theta\in\Theta_0$のとき

$\frac{\pi_0g_0(\theta)f(x|\theta)}{m_{\pi}(x)}$

であり、$\theta\in\Theta_1$のとき

$\frac{(1-\pi_0)g_1(\theta)f(x|\theta)}{m_{\pi}(x)}$

となります。

よって、データが与えられた上での仮説を満たす確率$P(H_i|X)$は、その積分値

$P(H_0|X)=\int_{\Theta_0}\frac{\pi_0g_0(\theta)f(x|\theta)}{m_{\pi}(x)}d\theta$

$P(H_1|X)=\int_{\Theta_1}\frac{(1-\pi_0)g_1(\theta)f(x|\theta)}{m_{\pi}(x)}d\theta$

で与えられます。

従って、事後オッズ比は、

$\frac{P(H_0|X)}{P(H_1|X)}=\frac{\int_{\Theta_0}\frac{\pi_0g_0(\theta)f(x|\theta)}{m_{\pi}(x)}d\theta}{\int_{\Theta_1}\frac{(1-\pi_0)g_1(\theta)f(x|\theta)}{m_{\pi}(x)}d\theta}$

$=\frac{\frac{\pi_0}{m_{\pi}(x)}\int_{\Theta_0}g_0(\theta)f(x|\theta)d\theta}{\frac{1-\pi_0}{m_{\pi}(x)}\int_{\Theta_1}g_1(\theta)f(x|\theta)d\theta}$

$=\frac{\pi_0\int_{\Theta_0}g_0(\theta)f(x|\theta)d\theta}{1-\pi_0\int_{\Theta_1}g_1(\theta)f(x|\theta)d\theta}$

と計算できます。

ここで、$\pi_0$によらない部分、つまり

$\frac{\int_{\Theta_0}g_0(\theta)f(x|\theta)d\theta}{\int_{\Theta_1}g_1(\theta)f(x|\theta)d\theta}$

をベイズファクター$BF_{01}$と定義します。

よって事後オッズ比は、

$\frac{P(H_0|X)}{P(H_1|X)}=\frac{\pi_0}{1-\pi_0}BF_{01}$

と表すことができます。

事後分布によって決められる事後オッズ比に対して、$\frac{\pi_0}{1-\pi_0}$の部分は事前分布によって決められる事前オッズ比ということができます。

よって、この式は以下のように簡単に表すことができます。

事後オッズ比=事前オッズ比×ベイズファクター

検定の証拠の強さを表すとは

ベイズファクターは、仮説検定における証拠の強さを表すことができます。

Jeffreysはベイズファクターの証拠価値を次のように表現しています。

上記の表から、$BF_{01}$が0に近づけば近づくほど、帰無仮説を棄却するための証拠が強くなると言えます。

例えば、以下のような仮説検定を考えます。

$H_0:\theta\leq\theta_0$
$H_1:\theta\gt\theta_0$

事前オッズ比を$\frac{4}{1}$とするように事前分布を設定します。

これは、事前分布において帰無仮説を満たす確率が80%であるので、帰無仮説が非常に棄却されにくい状態で設定したということになります。

例えばベイズファクターが以下の場合を考えてみます。

⑴$BF_{01}=\frac{1}{30}$の場合

事後オッズ比は$\frac{4}{1}×\frac{1}{30}=\frac{1}{7.5} \gt \frac{1}{19}$

⑵$BF_{01}=\frac{1}{100}$の場合

事後オッズ比は$\frac{4}{1}×\frac{1}{100}=\frac{1}{25} \lt \frac{1}{19}$

$BF_{01}$の値が$\frac{1}{100}$もあれば、帰無仮説が非常に棄却されにくい状態で設定したとしても、帰無仮説を棄却することができます。

したがって、$BF_{01}$が0に近づけば近づくほど、帰無仮説を満たす確率を小さくするための割合が大きくなるので、棄却するための証拠が強くなっていると言えます。

例題

ベイズ統計と仮説検定【3】でも扱った例題で、ベイズファクターを用いて計算してみましょう。

例題

成人男性の平均身長が170cmより大きいかどうかを調べます。成人男性の身長は$N(\mu,10^2)$に従うとします。

ある男性のデータを確認したところ177cmでした。このとき成人男性の平均身長が170cm以下であるといえるでしょうか。

ただし、$\mu$は事前に$N(172,20^2)$に従うとし、しきい値を$\frac{1}{19}$とします。

ベイズ統計と仮説検定【3】より事後オッズ比は0.335であると算出しました。

事前オッズ比を算出します。

$\pi_0=P(\mu\leq170)=\Phi(\frac{170-172}{20})=\Phi(-0.1)=0.460$

$1-\pi_0=1-0.460=0.540$

上記より、事前オッズ比は次のようになります。

$\frac{\pi_0}{1-\pi_0}=\frac{0.460}{0.540}=0.852$

よってベイズファクターは次のようになります。

$BF_{01}=\frac{0.335}{0.852}=0.393$

表から、帰無仮説を支持することに反対する証拠がほとんどない、という結果が得られます。

関連記事

第1回：ベイズ統計と仮説検定【1】～頻度論との違い～
第2回：ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～
第3回：ベイズ統計と仮説検定【3】～頻度論の考え方に基づくベイズ統計の仮説検定～
第4回：ベイズ統計と仮説検定【4】～ベイズファクター～
第5回：ベイズ統計と仮説検定【5】～点帰無仮説におけるベイズ流の仮説検定～
第6回：ベイズ統計と仮説検定【6】～ベイズ流仮説検定の問題点～