ベイズ統計と仮説検定2～ベイズ統計の基本的な仮説検定～

ベイズ統計における仮説の棄却と受容

第1回の「ベイズ統計と仮説検定①～頻度論との違い～」では、ベイズ統計においてデータが得られた上で帰無仮説を満たす確率が$P(H_0|X)$であることを説明しました。

ここからは、どのように仮説検定を進めるかを説明します。

例えば、帰無仮説$H_0$、対立仮説$H_1$を以下のようにおきます。

$H_0:\theta\leq\theta_0$
$H_1:\theta\gt\theta_0$

また、データを得た後の事後分布が次にのようになったとします。

データを得たもとでの$H_0$、$H_1$を満たす確率はそれぞれ以下のようになります。

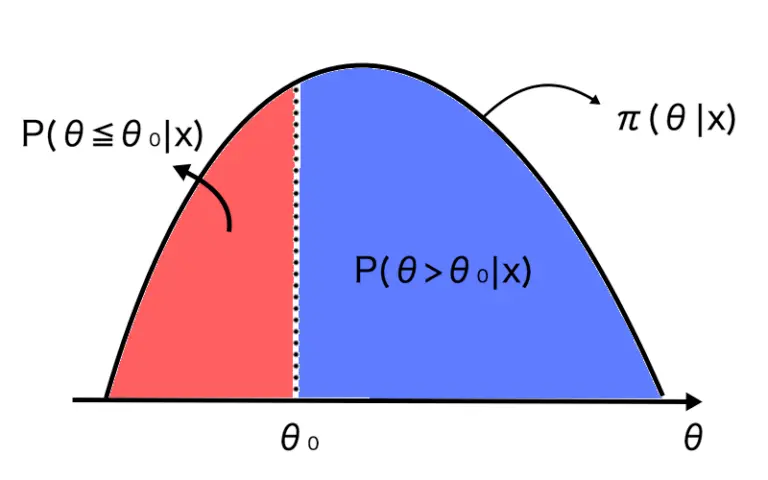
赤い部分が$P(H_0|X)$、青い部分が$P(H_1|X)$です。青い部分の方が、赤い部分よりも確率が大きいです。

つまり、データを得たもとでの帰無仮説$H_0$を満たす確率よりも、対立仮説$H_1$を満たす確率の方が大きいと言えます。

よって、帰無仮説$H_0$を棄却し、対立仮説$H_1$を採択します。

従来の仮説検定では、「帰無仮説を棄却しない＝帰無仮説が正しいと判断する」ということは言えませんでしたが、仮説が成り立つ確率を直接算出するベイズ統計の検定では、このことが成立します。

ベイス統計における仮説検定の例題

では、実際に例題を用いてベイズ統計における仮説検定を考えましょう。

例題

1枚のコインがあります。このコインを5回投げたところ、表が4回出ました。このコインの表の出る確率は$\frac{1}{2}$以下と言えるでしょうか。

ただし、事前のデータで、表の出る確率は$Beta(\frac{1}{2},\frac{1}{2})$に従っているとします。

表の出る確率をpとし、帰無仮説と対立仮説を以下のように設定します。

$H_0:p\leq\frac{1}{2}$
$H_1:p\gt\frac{1}{2}$

事前分布は$\pi(p)$は$Beta(\frac{1}{2},\frac{1}{2})$に従っているので、事後分布$\pi(p|x)$は平均$\frac{3}{4}$の$Beta(\frac{9}{2},\frac{3}{2})$に従います。

補足

事前分布が$Beta(\alpha,\beta)$に従っているとき、事後分布は、

平均：$frac{\alpha+x}{\alpha+\beta+n}$

分散：$\frac{(\alpha+x)(\beta+n-x)}{(\alpha+\beta+n)^2(\alpha+\beta+n+1)}$

のベータ分布$Beta(\alpha+x,\beta+(n-x))$に従う。ただし、$x$は表の出た回数である。

詳細は「ベルヌーイ分布の事後分布の平均と分散」をご確認ください。

グラフにすると以下のようになります。

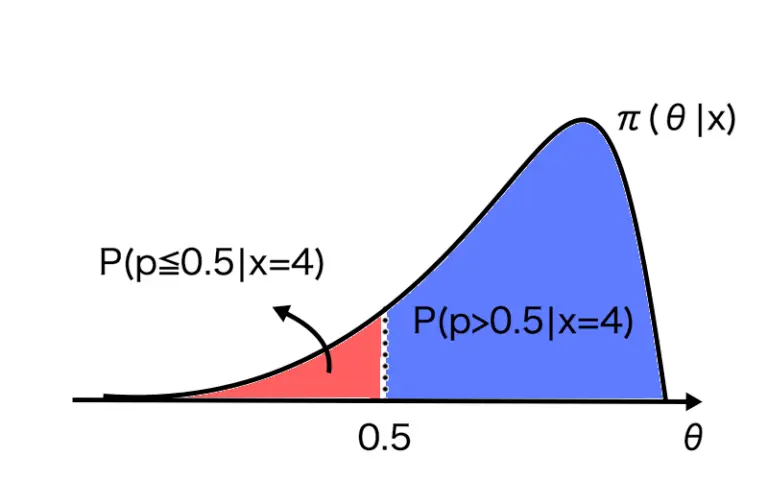
よって、帰無仮説$H_0$を満たす確率よりも、対立仮説$H_1$を満たす確率の方が大きいので、帰無仮説を棄却し、対立仮説を採択します。

よって、表の出る確率は$\frac{1}{2}$よりも上である、と判断します。（厳密には、積分して確率を求めましょう。）

まとめ

ベイズ統計における仮説検定では、仮説が成り立つ確率を直接計算して検定を行います。これが従来の仮説検定との大きな違いとなります。

関連記事

第1回：ベイズ統計と仮説検定【1】～頻度論との違い～
第2回：ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～
第3回：ベイズ統計と仮説検定【3】～頻度論の考え方に基づくベイズ統計の仮説検定～
第4回：ベイズ統計と仮説検定【4】～ベイズファクター～
第5回：ベイズ統計と仮説検定【5】～点帰無仮説におけるベイズ流の仮説検定～
第6回：ベイズ統計と仮説検定6～ベイズ流仮説検定の問題点～