分散とは？2種類の公式と計算例を解説

分散とは（Variance）

分散とは数値データのばらつき具合を表すための指標です。ある一つの群の数値データ（観測値）において、個々のデータと平均値の差の2乗の平均を求めることによって計算されます。

分散を文字式で表す場合、標本分散を$s^2$、母分散を$σ^2$と表現することが多いです。

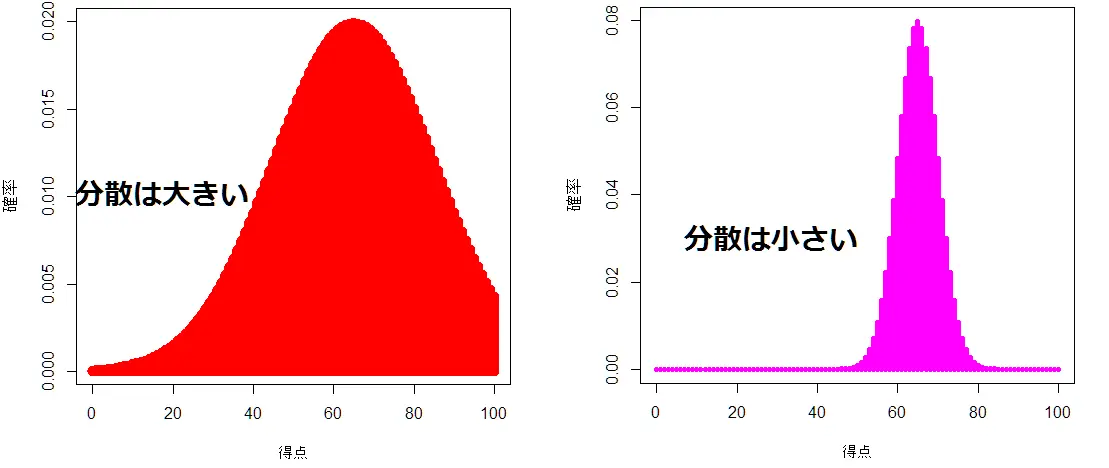
分散には、平均値から離れたデータが多ければ分散は大きくなり、平均値に近いデータが多ければ分散は小さくなるという特徴があります。

分散の公式

分散はデータと平均値の差の2乗の平均であることから、公式は以下のようになります。

$s^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2$

$n$：データの数
$x_i$：各データ($x_1,x_2…x_n$)
$\overline{x}$：データの平均

また、分散はデータと平均の差の2乗の期待値という見方もできます。

このことから確率変数$X$の分散$Var[X]$は、平均$μ$を用いて、以下のように表されます。

$Var[X] = E[(X-μ)^2]$

分散が2乗の和の平均をとる理由

データと平均の差$(\overline{x}-x_1),(\overline{x}-x_2)…(\overline{x}-x_n)$は、それぞれのデータが平均値からどれだけ離れているかを表す指標（偏差）です。

上記の計算では、正と負の両方の値をとる可能性があるため、そのまま足すと相殺されてしまい、平均値からどれだけ離れているか表す指標として適切ではありません。

そこで偏差を2乗することで、偏差が負の値をとったとしても平均値からのばらつきの基準を正負によらない値に統一できるのです。

文字式でも、2乗を用いて$s^2$ や $σ^2$のように表現されます。

また、単に$s$ や $σ$と表される値は、分散の平方根をとった値として標準偏差と呼ばれます。

シンプルな分散の算出方法

データと平均値の差の2乗の平均のほかに、モーメントを使って「2乗の期待値 - 期待値の2乗」で算出する方法もあります。

$V[X] = E(X^2) - [E(X)]^2 = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i^2 -[\frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i]^2$

上記の式を期待値の線形性を用いて導出すると以下のように証明できます。

$$\begin{equation*}\begin{split}Var[X]  &= E[(X-μ)^2]\\ &= E[X^2-2μX+μ^2] \\ &= E[X^2] -　2μE[X] + μ^2 \\ &=E[X^2] -　2μ×μ + μ^2\\ &=E[X^2] - μ^2\\&=E[X^2] - (E[X])^2 \end{split}\end{equation*}$$

分散の計算例

Aさん,Bさん,Cさん,Dさん,Eさんの数学のテストの得点がそれぞれ以下のようになりました。このデータの分散を求めてみましょう。

通常の公式での計算例

データと平均値の差の２乗の平均を用いて求めてみましょう。

まずは平均を算出します。

$\frac{90+80+40+60+90}{5} = 72$

よって分散は以下のように求められます。

$V[X] = \frac{(90-72)^2+(80-72)^2+(40-72)^2+(60-72)^2+(90-72)^2}{5} = 376$

シンプルな方法での計算例

モーメントを使って「2乗の期待値 - 期待値の2乗」でも分散をしてみましょう。

まずは、2乗の期待値$E(X^2)$ を計算します。

$E(X^2) = \frac{90^2+80^2+40^2+60^2+90^2}{5} = 5560$

次に、期待値の2乗$[E(X)]^2$ を計算します。

期待値は上記で求めた平均と同じ値になるので、

$[E(X)]^2 = 72^2 = 5184$

最後に 2乗の期待値 - 期待値の2乗を計算します。

$V[X] = E(X^2) - [E(X)]^2 = 5560 - 5184 = 376$

関連記事

標準偏差の公式と計算例