平均値とは

平均値とは

平均値とは複数の数値に対して、個々を全て足し合わせた後、数値の個数で割った値のことを指します。統計データを代表する値としてよく使われています。

文字式で表す際、文字の上にバーをつけて$\overline{x}$ や $μ$ と表されます。

計算例

Aさん,Bさん,Cさん,Dさん,Eさんの数学のテストの得点がそれぞれ以下のようになりました。

この場合、平均の得点は以下となります。

$\frac{90+80+40+60+90}{5} = 72$

平均を求める公式

平均値を求める式を数字だけではなく、文字式でも表してみましょう。

ここでは、$n$個の観測数値データを分かりやすくするために、$x_1,x_2…x_n$と置くことにします。$x$の添字は観測したデータの番号を表しています。これらの観測値の平均$\overline{x}$は次の式で表されます。

$\overline{x} = \frac{1}{n}(x_1+x_2+…+x_n) = \frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } x_i$

平均と重心の関係

平均は、観測値の重心を表す指標として使われることが多いです。

例えば観測値が３個であった場合、$n=3$であるので、以下となります。

$\overline{x} = \frac{1}{3}(x_1+x_2+x_3)$

この式は、三角形の重心の座標を求める式と同じです。つまり、観測値が３個である場合、平均とは観測値の重心であるということが分かります。

また、観測値が増えた場合でも、観測データが左右対称であれば、平均値というのはまさに観測データの重心を表すことになるでしょう。データが左右対称でない場合、平均値というのは、観測値の中心からずれることになります。

つまりデータの対称性が強ければ、平均値はデータの中心を指す指標として大きな意味を持ちますが、逆に非対称性が強い場合は中心を指す指標としては弱くなってしまいます。その場合は、中央値や最頻値などもデータを判断する上の良い材料となります。

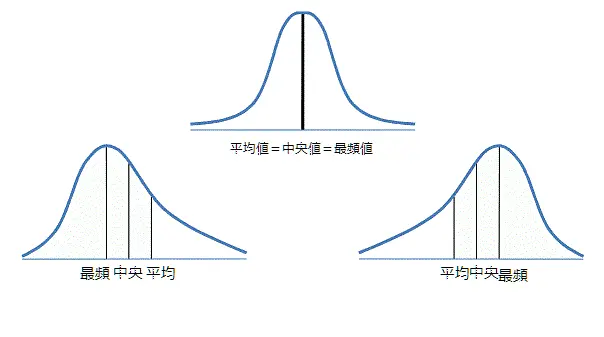
また、完全対象な観測値である場合、平均値、最頻値、中央値は同じ値を取ります。