中心極限定理の例とメリットを分かりやすく解説

中心極限定理とは

中心極限定理は、以下のように定義されます。

平均$\mu$、分散$\sigma^2$をもつあらゆる分布からの無作為標本の標本平均$X$の分布はnが十分大きいとき以下の式が成立する。

$\lim_{n \to \infty} P(Z_{n} \leq z)=\Phi(z)=\int_\infty^z \frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}} dx$

まず、どのような分布に従うかわからない母集団から、無作為に抽出した標本を$X_{1},X_{2}、、、、、,X_{n}$します。

中心極限定理とは、このnが十分に大きい時を考えるとき、以下の式が成立して良いことにする定理なのです。

$S_{n}=X_{1}+X_{2}+、、、、+X_{n} \overset{}{\sim} N(n \mu,n \sigma^2)\\\overline{X}=X_{1}+X_{2}+、、、、+X_{n}/n\overset{}{\sim} N(\mu,\sigma^2/n)$

サイコロを例に中心極限定理を考える

上の式を見ても中心極限定理の概念を理解することは難しいので、サイコロを用いた一様分布の例を用いて考えます。

サイコロの目が出る確率は一様に$\frac{1}{6}$です。

次に、サイコロを6回投げたときの出た目の合計を考えます。合計はどのくらいになると考えるのが自然でしょうか。

サイコロを一回投げた時の目の期待値（平均値）は、$E(X)=(1+2+3+4+5+6)/6=\frac{7}{2}$です。

6回サイコロを投げる試行を繰り返したとき、合計値が$\frac{7}{2}×6=21$になる可能性が一番高そうであると想像できます。

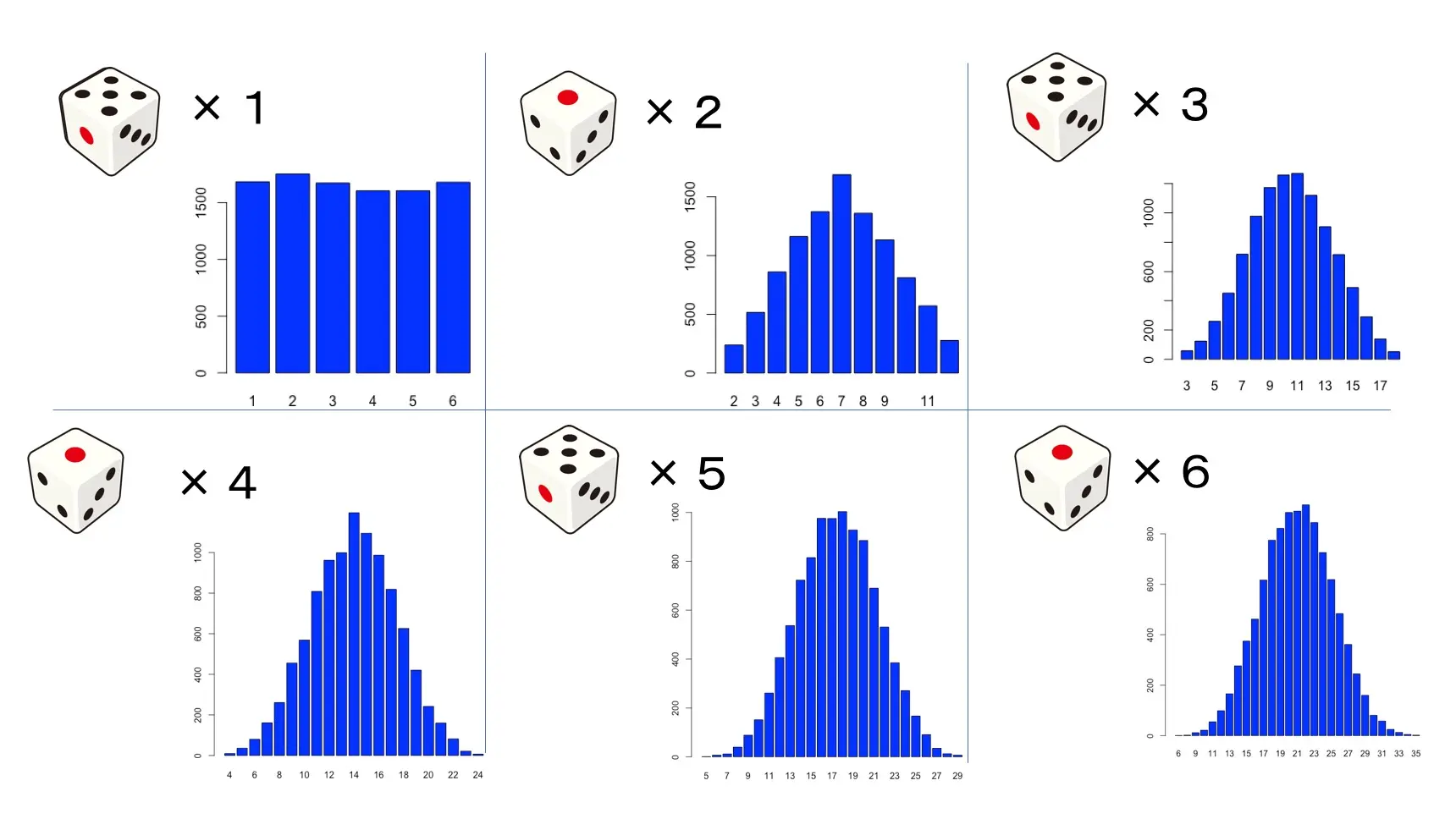
上記図から、サイコロを振った回数が2回以降の確率分布が正規分布のような形になっており、サイコロの目の和$S_{n}$が正規分布に近似できることが感覚的に理解できるかと思います。

正規分布のままではパラメータによって数値が変動するため、標準化してより扱いやすい形にしてみましょう。

$\overline{X} \overset{}{\sim} N(n\mu,\sigma^2/n)$

$\overline{X}-\mu \overset{}{\sim} N(0,\sigma^2/n)$

$\frac{\overline{X}-\mu}{\sigma/\sqrt{n}} \overset{}{\sim} N(0,1)$

これにより、確率変数$\frac{\overline{X}-\mu}{\sigma/\sqrt{n}}$は標準正規分布に従うことがわかるため、以下を導出できます。

$$\begin{equation*}\begin{split}\lim_{n \to \infty} P(Z_{n} \leq z)=\Phi(z)=\int_\infty^z \frac{1}{\sqrt{2\pi}}\mathrm{e}^{-\frac{x^2}{2}} dx\end{split}\end{equation*}$$

中心極限定理のメリット

中心極限定理のメリットを、例題を解きながら見ていきましょう。

【例題】

サイコロを100回振った時、その目の和が300以上420以下となる確率を求めよ。

中心極限定理を使わない場合、300から420まで、それぞれの目の和の確率を算出していく必要があります。
中心極限定理を使えば、算出の手間を省くことができます。

【解答】

サイコロの出る目$X$は$\mu=\frac{7}{2}$、$\sigma^2=\frac{35}{12}$の離散一様分布に従う。

出る目の和$S_{n}=X_{1}+X_{2}+,...,+X_{n}$は、中心極限定理の

$S_{n}=X_{1}+X_{2}+,...,+X_{n} \overset{}{\sim} N(n \mu,n \sigma^2)$

を適用すると、

$S_{n}\overset{}{\sim} N(350,\frac{3500}{12})$

が言える。これを標準化すると、

$S_{n}-350 \overset{}{\sim} N(0,\frac{3500}{12})$

$\frac{S_{n}-350}{\sqrt{\frac{3500}{12}}} \overset{}{\sim} N(0,1)$

$$\begin{equation*}\begin{split}P(300\leq S_{n} \leq 420)&=P(\frac{300-350}{\sqrt{\frac{3500}{12}}} \leq \frac{S_{n}-350}{\sqrt{\frac{3500}{12}}} \leq \frac{420-350}{\sqrt{\frac{3500}{12}}})\\&=P(-\frac{50}{17.08} \leq \frac{S_{n}-350}{\sqrt{\frac{3500}{12}}} \leq \frac{70}{17.08})\\&=P(-2.93 \leq \frac{S_{n}-350}{\sqrt{\frac{3500}{12}}} \leq 4.10)\\&=1-0.0017-0.00002\\&=0.9981\end{split}\end{equation*}$$

関連記事

正規分布の公式と特徴まとめ

正規分布を標準化して標準正規分布にする方法