ベイズ統計と仮説検定5～点帰無仮説におけるベイズ流の仮説検定～

点帰無仮説におけるベイズ流仮説検定の問題点

以下のような仮説検定を考えます。

$H_0:\theta=\theta_0$
$H_1:\theta\neq\theta_0$

連続型の事前分布を$\pi(\theta)$とすると、点帰無仮説を満たす事前確率は以下の図のようになります。

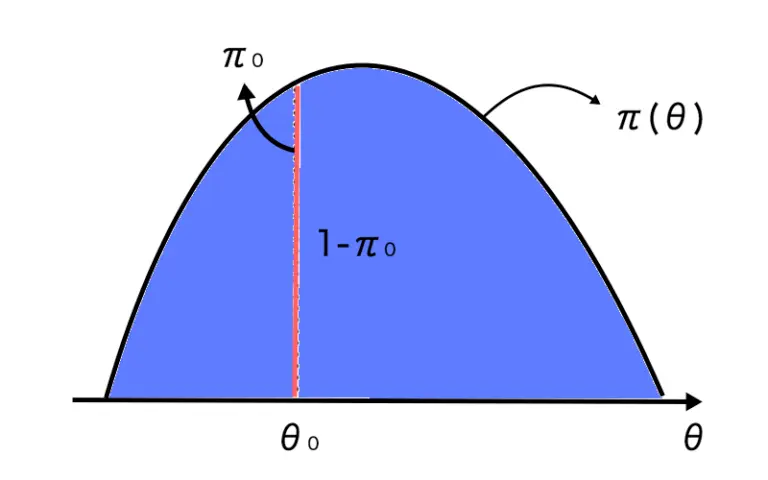
点帰無仮説は幅がないため、帰無仮説を満たす確率$\pi_0$が0になってしまいます。

もちろん事後分布における事後確率も0になり、検定ができなくなってしまうのが点帰無仮説におけるベイズ流仮説検定の問題点です。

そこで、点帰無仮説におけるベイズ流仮説検定では、帰無仮説を満たす事前確率$\pi_0$を自分で割り当てて検定を行います。

例えば、日本人の成人男性の平均身長において、以下のような仮説検定を考えます。

$H_0:\mu=170$
$H_1:\mu\neq 170$

理論上は$\mu=170$を満たす確率は0ですが、例えばこれを50％とおきます。

つまり、$\mu=170$である確率が50%、$\mu\neq 170$である確率が50%と仮定して仮説検定を行います。

事後オッズ比とベイズファクターの計算

点帰無仮説の場合、ベイズ統計と仮説検定【4】で扱った事前分布

$\pi(\theta)=\pi_0g_0(\theta)I(\theta\in\Theta_0)+(1-\pi_0)g_1(\theta)I(\theta\in\Theta_1)$

は、次のように書き換えられます。

$\pi(\theta)=\pi_0(\theta)I(\theta=\theta_0)+(1-\pi_0)g_1(\theta)I(\theta\neq\theta_0)$

周辺尤度は次のように計算できます。

$m(x)=\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)$

$m_1(x)=\int_{\theta\neq\theta_0}f(x|\theta)g_1(\theta)d\theta$

よって事後確率は

$\pi(\theta_0|x)=\frac{f(x|\theta_0)\pi_0}{m(x)}$

$=\frac{\pi_0f(x|\theta_0)}{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}$

$=[\frac{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}{\pi_0f(x|\theta_0)}]^{-1}$

$=[1+\frac{1-\pi_0}{\pi_0}\frac{m_1(x)}{f(x|\theta_0)}]^{-1}$

$1-\pi(\theta_0|x)=1-\frac{f(x|\theta_0)\pi_0}{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}$

$\frac{(1-\pi_0)m_1(x)}{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}$

したがって事後分布は、以下のようになります。

$\frac{\pi(\theta_0|x)}{1-\pi(\theta_0|x)}=\frac{\frac{\pi_0f(x|\theta_0)}{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}}{\frac{(1-\pi_0)m_1(x)}{\pi_0f(x|\theta_0)+(1-\pi_0)m_1(x)}}$

$=\frac{\pi_0}{1-\pi_0}\frac{f(x|\theta_0)}{m_1(x)}$

ここで$\pi_0$によらない部分

$BF_{01}=\frac{f(x|\theta_0)}{m_1(x)}$

をベイズファクターとして定義するので、事後確率$\pi(\theta_0|x)$は次のようになります。

$\pi(\theta_0|x)=[1+\frac{1-\pi_0}{\pi_0}BF_{01}^{-1}]^{-1}$

例題：二項分布の場合のベイズファクター

例として、二項分布の場合のベイズファクターを計算してみましょう。

例題

$H_0:p=p_0$
$H_1:p\neq p_0$

という検定を考える。データは$X〜B(n,p)$であるとする。このとき、事前分布は$p〜Beta(\alpha,\beta)$に従うとする。

上記の理論における$m_1(x)$は

$m_1(x)= \binom{n}{x}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\frac{\Gamma(\alpha+x)\Gamma(\beta+n-x)}{\Gamma(\alpha+\beta+n)}$

であるから、ベイズファクターは

$BF_{01}=\frac{\binom{n}{x}\theta_0^x(1-\theta_0)^{n-x}}{\binom{n}{x}\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\frac{\Gamma(\alpha+x)\Gamma(\beta+n-x)}{\Gamma(\alpha+\beta+n)}}$

$=\frac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}\frac{\Gamma(\alpha+\beta+n)}{\Gamma(\alpha+x)\Gamma(\beta+n-x)}\theta_0^x(1-\theta_0)^{n-x}$

と計算できます。

よって、事後確率は

$\pi(\theta_0|x)=[1+\frac{1-\pi_0}{\pi_0}BF_{01}^{-1}]^{-1}$

$=[1+\frac{1-\pi_0}{\pi_0}\frac{\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}\frac{\Gamma(\alpha+x)\Gamma(\beta+n-x)}{\Gamma(\alpha+\beta+n)}}{\theta_0^x(1-\theta_0)^{n-x}}]^{-1}$

例題：点帰無仮説の場合の仮説検定

例題を用いて、点帰無仮説の場合の仮説検定を考えてみましょう。

例題

コインを5回投げたところ4回表が出ました。このコインはイカサマコインと言えるでしょうか。

ただし表の出る確率の分布は事前に$Beta(1,1)$に従っているとし、しきい値を$\frac{1}{19}$とします。

表の出る確率をpとし、以下の仮説検定を考えます。

$H_0:p=\frac{1}{2}$
$H_1:p\neq \frac{1}{2}$

先ほどの例題「二項分布の場合のベイズファクター」で扱った式に代入すると、ベイズファクターは次のように表せます。

$BF_{01}=\frac{\Gamma(1)\Gamma(1)}{\Gamma(1+1)}\frac{\Gamma(1+1+5)}{\Gamma(1+4)\Gamma(1+5-4)}(\frac{1}{2})^4(1-\frac{1}{2})^{5-4}$

$=\frac{6!}{4!1!}(\frac{1}{2})^{5}$

$=\frac{15}{16}=0.9375$

よって$\pi_0=\frac{1}{2}$と割り当てると、事後オッズ比は次のようになります。

$\frac{P(H_0|X)}{P(H_1|X)}=\frac{\pi_0}{1-\pi_0}BF_{01}=\frac{\frac{1}{2}}{1-\frac{1}{2}}×0.9375=0.9375\lt\frac{1}{19}$

よって、帰無仮説を受容し、イカサマコインではないと判断します。また、ベイズファクターの値から帰無仮説に反対する根拠があまりないという結果が得られます。

補足

事後オッズ比の値から、$\theta_0$を満たす確率は$\frac{0.9375}{1+0.9375}=0.484=48.4\%$となっています。

これは、はじめ表の出る確率を50%と設定したが、「5回中4回表が出た」というデータから、表の出る確率が48.4%に落ちた、と解釈することができます。

関連記事

第1回：ベイズ統計と仮説検定【1】～頻度論との違い～
第2回：ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～
第3回：ベイズ統計と仮説検定【3】～頻度論の考え方に基づくベイズ統計の仮説検定～
第4回：ベイズ統計と仮説検定【4】～ベイズファクター～
第5回：ベイズ統計と仮説検定【5】～点帰無仮説におけるベイズ流の仮説検定～
第6回：ベイズ統計と仮説検定【6】～ベイズ流仮説検定の問題点～