ベイズ統計と仮説検定3～頻度論の考え方に基づくベイズ統計の仮説検定～

ベイズ統計に基づく仮説検定の課題

第2回ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～で説明したベイズ統計における仮説検定には課題があります。

ベイズ統計における仮説検定では、仮説が成り立つ確率を直接計算して検定を行います。

そこで、以下のような図を例に考えてみます。

帰無仮説$H_0$を満たす確率が40%、対立仮説$H_1$を満たす確率が60%です。

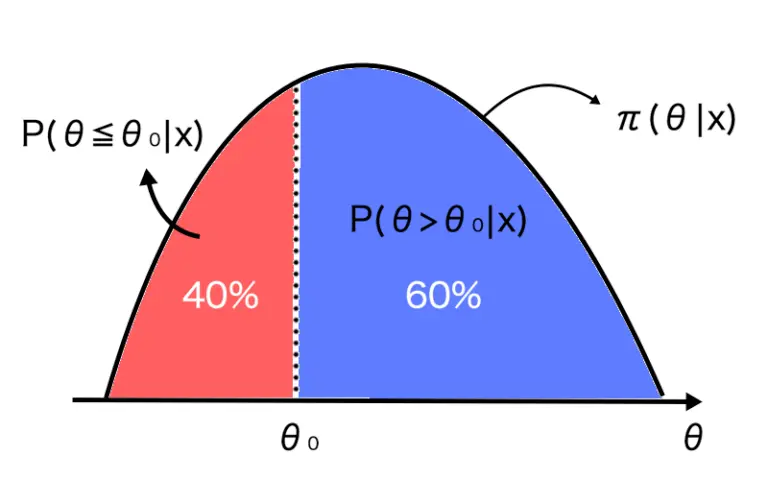
上図から、ベイズ統計における仮説検定で考えると「確率が低い帰無仮説を棄却する」という結論になります。

しかし、帰無仮説を満たす確率は40%あり、決して低い確率とは言えません。従来の頻度論の仮説検定における「やむを得ない理由がない限り、帰無仮説を棄却すべきではない」という考え方に反しています。

以降では、上記の課題を踏まえて頻度論の考え方に基づくベイズ統計の仮説検定について説明します。

従来の仮説検定のおさらい

従来の仮説検定の考え方は、ネイマン-ピアソン流の以下のような考え方です。

①第1種の過誤の確率を一定以下（主に5%など）に抑えながら
②第2種の過誤の確率を小さくする

第1種の過誤の確率は、「帰無仮説が正しいのにも関わらず、帰無仮説を棄却してしまう確率」であり、①を満たすことが従来の仮説検定の前提条件になります。

この前提条件から、「あまりにもおかしなデータが得られない限り、帰無仮説を棄却するのは避けよう」という考えが見えてきます。

これが初めに書いた「やむを得ない理由がない限り、帰無仮説を棄却すべきではない」という考え方につながっています。

頻度論の考え方に基づくベイズ流仮説検定

冒頭で説明したベイズ統計に基づく仮説検定では、「第1種の過誤の確率を一定以下（主に5%など）に抑える」という前提条件を満たしません。

頻度論の考え方に基づくベイズ流仮説検定では、帰無仮説を満たす確率を一定以下に抑えることを考えます。

従来の仮説検定では有意水準を5%とし検定を行うのがメジャーであるので、今回のベイズ流仮説検定でも「帰無仮説を満たす確率」を5%以下に抑えることを考えていきます。

ここで事後オッズ比という概念を導入します。

事後オッズ比

事後オッズ比は、事後分布において「対立仮説を満たす確率よりも、帰無仮説を満たす確率がどのくらい大きいか」を表す。

$\frac{P(H_0|X)}{P(H_1|X)}$

上の例でいうと、事後オッズ比は以下で計算できます。

$\frac{P(H_0|X)}{P(H_1|X)}=\frac{40\%}{60\%}=\frac{0.4}{0.6}=\frac{2}{3}$

この事後オッズ比が、$\frac{1}{19}$以下の場合に帰無仮説を棄却し、$\frac{1}{19}$より上の場合に帰無仮説を受容します。

$\frac{1}{19}$が基準となる理由は以下のグラフで確認できます。

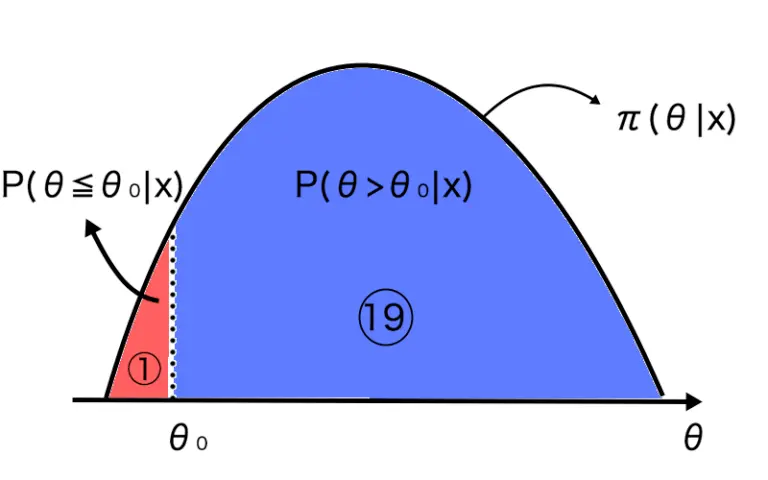
$100\%×\frac{1}{1+19}=5\%$で、赤い部分の確率が5%になっていることが分かります。

つまり、事後オッズ比が$\frac{1}{19}$以下なら、帰無仮説を満たす確率が5%以下であると言えるのです。

例題

実際に例題を用いて考えてみましょう。

例題

成人男性の平均身長が170cmより大きいかどうかを調べます。成人男性の身長は$N(\mu,10^2)$に従うとします。

ある男性のデータを確認したところ177cmでした。このとき成人男性の平均身長が170cm以下であるといえるでしょうか。

ただし、$\mu$は事前に$N(172,20^2)$に従うとし、しきい値を$\frac{1}{19}$とします。

帰無仮説$H_0$と対立仮説$H_1$を以下のようにおきます。

$H_0:\mu\leq170$
$H_1:\mu\gt170$

事後分布の平均、分散は次のように計算できます。

母平均$\mu$、母分散$\sigma^2$に従う正規母集団から大きさ$n$の標本を抽出し、標本平均$\overline{x}$を得たとします。

母平均$\mu$の事前分布として平均$\eta$、分散$\tau^2$の正規分布をとるとき、$\mu$の事後分布は次の正規分布に従います。

平均

$\frac{n\tau^2\overline{x}+\sigma^2\eta}{n\tau^2+\sigma^2}=\frac{\frac{n}{\sigma^2}\overline{x}+\frac{1}{\tau^2}\eta}{\frac{n}{\sigma^2}+\frac{1}{\tau^2}}$

分散

$\frac{\tau^2\sigma^2}{n\tau^2+\sigma^2}=\frac{\frac{\sigma^2\tau^2}{n}}{\frac{\sigma^2}{n}+\tau^2}$

（詳細は「正規分布の事後分布の平均と分散」をご確認ください。）

事後分布の平均、分散は以下となります。

事後分布の平均：176

事後分布の分散：80

標準化することにより、以下が得られます。

$P(\mu\leq 170|X=177)=\Phi(\frac{170-176}{\sqrt{80}})=\Phi(-0.671)=0.251$

$P(\mu\gt 170|X=177)=1-0.251=0.749$

よって、事後オッズ比は以下となります。

$\frac{P(H_0|X)}{P(H_1|X)}=\frac{0.251}{0.749}=0.335$

0.335は$\frac{1}{19}$よりも大きいので、「帰無仮説を受容し、成人男性の平均身長は170cmより大きいとは言えない」と判断します。

関連記事

第1回：ベイズ統計と仮説検定【1】～頻度論との違い～
第2回：ベイズ統計と仮説検定【2】～ベイズ統計の基本的な仮説検定～
第3回：ベイズ統計と仮説検定【3】～頻度論の考え方に基づくベイズ統計の仮説検定～
第4回：ベイズ統計と仮説検定【4】～ベイズファクター～
第5回：ベイズ統計と仮説検定【5】～点帰無仮説におけるベイズ流の仮説検定～
第6回：ベイズ統計と仮説検定【6】～ベイズ流仮説検定の問題点～