t分布とは

t分布とは

確率変数$Z$が標準正規分布$N(0,1)$、確率変数$W$が自由度$n$のカイ二乗分布に従うとき、

$t = \frac{Z}{\sqrt{\frac{W}{n}}}$

と表される$t$が従う分布を、t分布といいます。

t分布の公式

t分布表

t分布の〇〇以上の値をとる確率を一覧にしたものがt分布表といいます。この表はt検定などで頻繁に使うので、見方を覚えておきましょう。

詳細は「片側t分布表と見方」をご確認ください。

t分布の性質

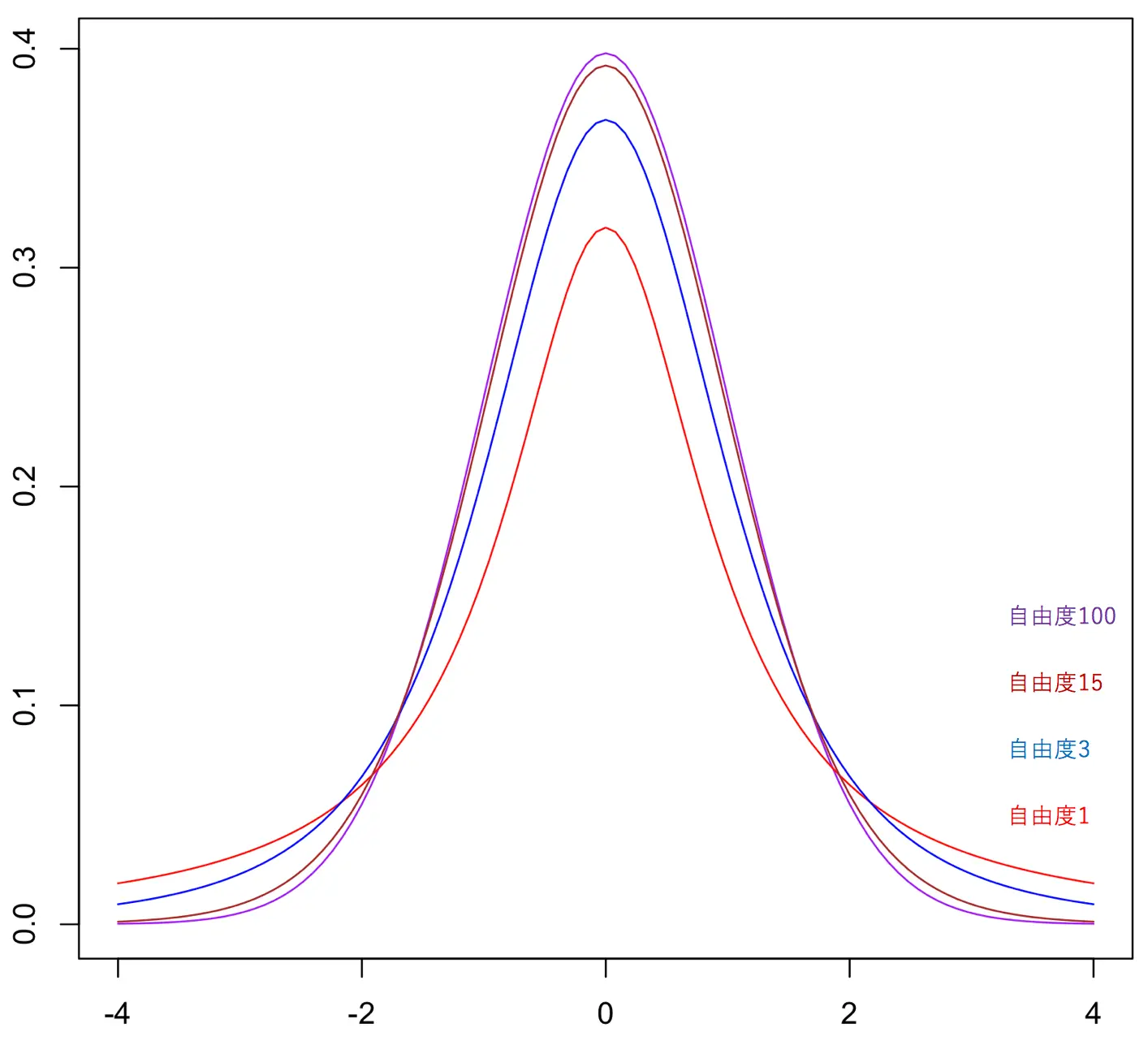
t分布は自由度が大きくなるにつれ、標準正規分布の形に近づいていきます。

以下は、自由度1、自由度3、自由度15、自由度100のt分布の確率密度関数を比較したものです。

自由度が大きくなるにつれて、標準正規分布のグラフに近づいていくことが分かります。

カイ二乗分布・正規分布との関係

t分布はカイ二乗分布や正規分布と深い関係性があります。

正規分布$N(μ,σ^2)$に従う大きさ$n$の無作為標本$X_1,X_2,...,X_n$を考えたときに、

$W = \sum_{ i = 1 }^{ n } \frac{(X_i-\bar{X})^2}{σ^2}$

は自由度n-1のカイ二乗分布に従います。

これを、$t = \frac{Z}{\sqrt{\frac{W}{n}}}$の分母に代入すると、自由度n-1のt分布の式が完成し以下となります。

$$\begin{equation*}\begin{split}t &=\frac{Z}{\sqrt{\frac{\displaystyle \sum_{ i = 1 }^{ n } \frac{(X_i-\bar{X})^2}{σ^2}}{n-1}}} \\ \\&=\frac{\sqrt{n}(\bar{X}-μ)}{\sqrt{\frac{\displaystyle \sum_{ i = 1 }^{ n } (X_i-\bar{X})^2}{n-1}}}\\ \\&=\frac{\sqrt{n}(\bar{X}-μ)}{S}\end{split}\end{equation*}$$

$S^2$は不偏分散$\frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2$

これは、正規分布に従うと仮定した標本について、分散を不偏分散によって標準化すると、自由度n-1のt分布に従うということを表しています。

正規分布に従うと仮定した仮説検定は、母分散が未知の場合、t分布に標準化して行うので、t検定と言います。

関連記事

片側t分布表と見方

確率密度関数を用いたt分布の期待値の導出

カイ二乗分布のわかりやすいまとめ

t検定とは？種類と手順を解説