標準偏差の公式と計算例をわかりやすく解説

標準偏差とは

標準偏差とは、分散の平方根にとることによって計算される値です。文字式では、分散の文字式から２乗を取って、$s$や $σ$と表されます。

$標準偏差 =\sqrt{分散}$

標準偏差の公式

標準偏差$s$ は分散$s^2$ を使って以下のように表されます。

$s = \sqrt{s^2}$

また、$n$個の観測値 $x_1,x_2…x_n$ とその標本平均$\overline{x}$を用いて次のように表されることもあります。

$s = \sqrt{\frac{1}{n}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}$

ここでいう標準偏差は標本標準偏差、分散は標本分散とします。

標準偏差の計算例

Aさん,Bさん,Cさん,Dさん,Eさんの数学のテストの得点がそれぞれ以下のようになりました。このデータの標準偏差を求めてみましょう。

標準偏差は分散の平方根であることを念頭において、以下のように計算を進めましょう。

①平均を算出

$\frac{90+80+40+60+90}{5} = 72$

②分散を算出

$s^2 = \frac{(90-72)^2+(80-72)^2+(40-72)^2+(60-72)^2+(90-72)^2}{5} = 376$

③標準偏差を算出

$s = \sqrt{376} ≒ 19.39071$

標準偏差を求める意義

分散も標準偏差も、観測したデータのばらつきを表現するという意味では同じ役割を果たします。

分散は、計算過程で2乗の操作があるため、大きな値になる傾向があります。上記の計算例から「Aさん,Bさん,Cさん,Dさん,Eさんの数学のテストの得点の分散は376である」と言われても、それが何を意味するのか直観的に分かりません。

標準偏差を用いると、分散の平方根をとり、観測したデータとスケールを揃えることになるので、データのばらつき具合を直観的に理解しやすくなります。

上記の計算例では、「Aさん,Bさん,Cさん,Dさん,Eさんの数学のテストの得点の標準偏差は19.3である」となり、平均点±19.3点の範囲におおよその人が含まれているのだなと理解することができます。

標準偏差と正規分布

下図は正規分布のグラフにおける、標準偏差$σ,2σ,3σ$が示す範囲を指しています。

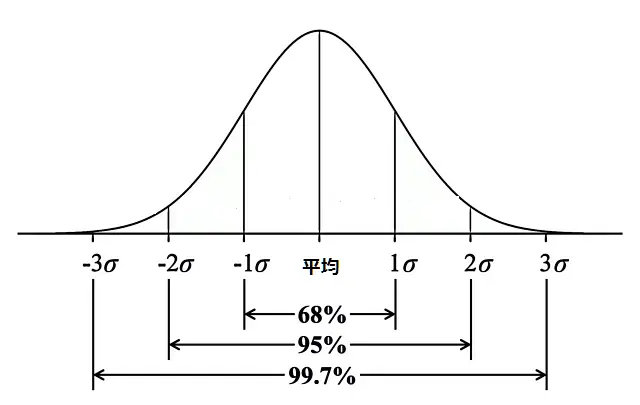
図のように、正規分布の場合、平均値±標準偏差中に観測データが含まれる確率は68.3%になります。これが±標準偏差の２倍、３倍になるとさらに確率は上がります。

特に、平均値±3σという範囲は、企業の商品製造の規格として広く採用されています。

不偏標準偏差

母標準偏差の推定値である不偏標準偏差$S$は不偏分散の平方根を取ることによって計算されます。

$S = \sqrt{\frac{1}{n-1}\displaystyle \sum_{ i = 1 }^{ n } (x_i-\overline{x})^2}$

標準偏差と偏差値

テストの結果でよく聞く偏差値の算出には、標準偏差が用いられています。

$偏差値＝\frac{(得点 - 平均点)}{\ \ \ \ \ 標準偏差\ \ \ \ \ }  ×10＋50$