F分布とは

F分布とは

$X$と$Y$が互いに独立である確率変数$X, Y$について、$X$が自由度$n$のカイ二乗分布、確率変数$Y$が自由度$m$のカイ二乗分布に従うと仮定します。

このとき、

$F = \frac{\frac{X}{n}}{\frac{Y}{m}}$

と表される$F$が従う分布を、F分布といいます。

F分布の確率密度関数

F分布の確率密度関数は以下となります。

$f(z) = \frac{(\frac{n}{m})^{\frac{n}{2}}}{B(\frac{n}{2}, \frac{m}{2})} \frac{z^{\frac{n}{2}-1}}{(1+\frac{n}{m}z)^{-\frac{n+m}{2}}}$

確率密度関数の導出は、「F分布の確率密度関数をカイ二乗分布を用いて導出」で説明しているのでご確認ください。

F分布の期待値と分散

F分布の期待値と分散は以下となります。

導出過程については、以下ページをご確認ください。

カイ二乗分布を用いたF分布の期待値と分散の導出

確率密度関数を用いたF分布の期待値と分散の導出

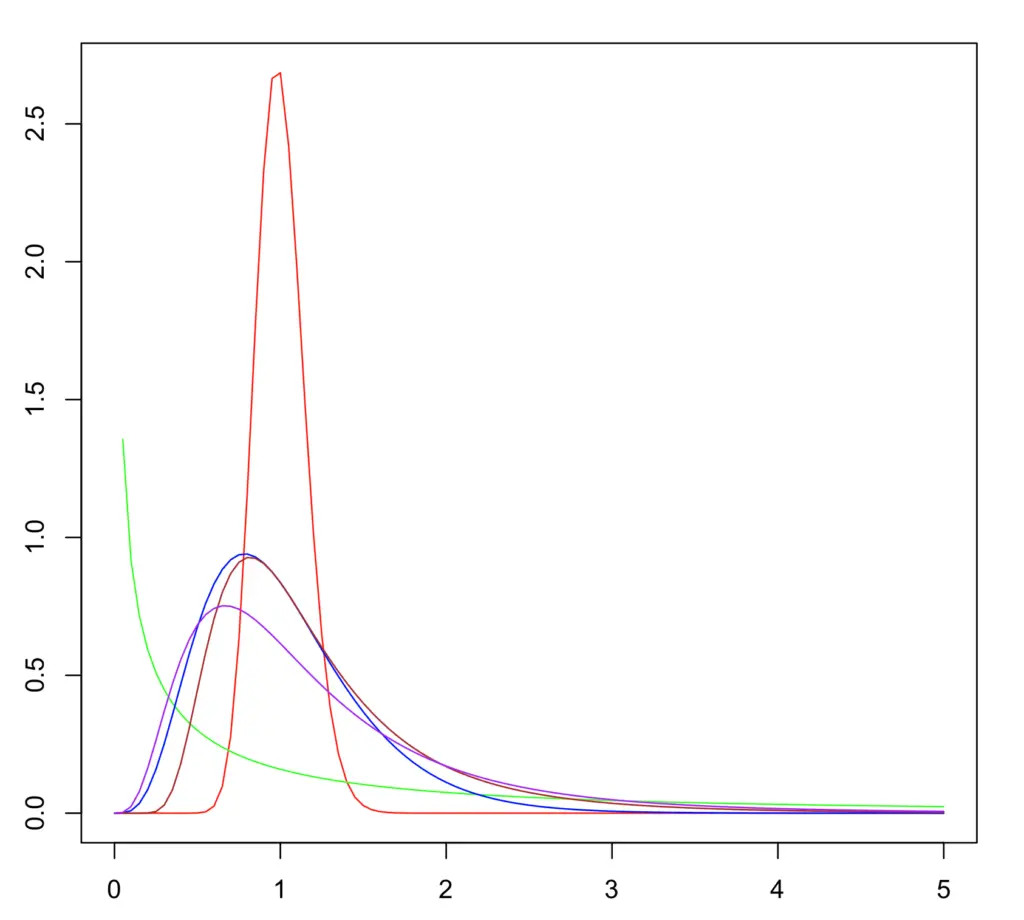
F分布のグラフの形

関連記事

カイ二乗分布のわかりやすいまとめ

F分布の確率密度関数をカイ二乗分布を用いて導出

カイ二乗分布を用いたF分布の期待値と分散の導出

確率密度関数を用いたF分布の期待値と分散の導出