見せかけの回帰について分かりやすく解説

見せかけの回帰とは

見せかけの回帰とは、２つの無関係な時系列データに関して回帰分析を行うと有意な相関が表れてしまう問題です。

回帰分析に用いる２つの時系列データがどちらも単位根過程に従うときに現れます。

見せかけの回帰の実例

以下の２つのランダムウォーク$x_{t},y_{t}$を用いて、「見せかけの回帰」を理解しましょう。

$x_{t} = 1 + x_{t-1} + \varepsilon_t$

$y_{t} = 1 + y_{t-1} + \zeta_t$

$\varepsilon_t ～ iid(0, 1)、\zeta_t ～ iid(0,1)$に従う。

まずは以下のグラフを見て２つのランダムウォーク、$x_{t}, y_t$の振る舞いを見てみましょう。

黒線が$x_{t}$、赤線が$y_t$を表しています。

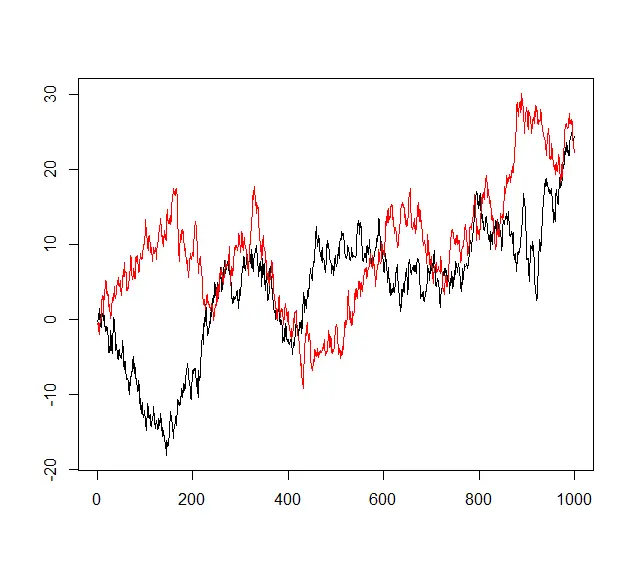
上記のグラフを見ると$x_{t},y_{t}$どちらもランダムに動いているように見えます。

この$x_{t},y_{t}$２つの間に有意な関係があるようには見えません。

実際に回帰分析をして確認してみましょう。以下が回帰分析の結果です。

xのt値が17.27であることを考えると$x_{t},y_{t}$の間に有意な関係が表れていると分かります。

確かに無関係であるはずの２つのランダムウォークに有意な関係が現れました。これが「見せかけの回帰」という現象です。

見せかけの回帰の対策

「見せかけの回帰」を回避する方法は主に２つあります。

方法①

$x_{t},y_{t}$それぞれの差分系列$\Delta x_t$、$\Delta y_t$を用いて回帰分析することです。

２つのランダムウォーク、$x_{t},y_{t}$の差分系列$\Delta x_t$、$\Delta y_t$は定常過程に従います。

以下の式変形を見ると$\Delta x_t$、$\Delta y_t$が定常過程に従うことが分かります。

$\Delta x_t = x_{t} - x_{t-1} = 1 + \varepsilon_t$　　$\Delta y_t = y_{t} - y_{t-1} = 1 + \zeta_t$

$\Delta x_t$、$\Delta y_t$はどちらも単位根過程ではないので、回帰分析をしても「見せかけの回帰」は起きません。

方法②

回帰式の説明変数にラグ変数、時差のある変数を追加することで「見せかけの回帰」を防ぐことができます。

例えば、$y_t$に対し$x_t$だけでなく$x_{t-1}$を説明変数に用いて回帰分析するということです。