ニューラルネットワークをわかりやすく解説

2024.4.09

2024.4.12

ニューラルネットワークとは

ニューラルネットワークとは、パーセプトロンを何層にも重ねたもので、多層パーセプトロンとも呼ばれます。

その原形は1943年に考案され、改良を繰り返すことでDeep Learningなど新たな手法が開発されるに至りました。

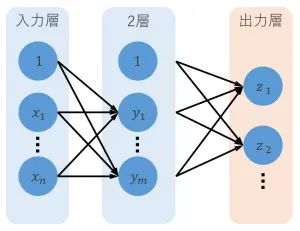
図を見るとニューラルネットワークが入力層、2層、出力層から構成されていることが分かります。この入力層、出力層以外の層を隠れ層と呼びます。今回は2層目が隠れ層になります。

1と書かれたノードはバイアスを表現するためのノードです。

このニューラルネットワークは $n$ 個の入力信号を受け取り、2層で $m$ 個のノードに変換、最後に $l \$ 個出力するとします。

ニューラルネットワークではどのノードもパーセプトロンと同じ働きをします。たくさんのパーセプトロンがつながり、重なることでニューラルネットワークを構築していることが分かります。

また、ノードが矢印でつながっています。

パーセプトロンの矢印が重みを持つようにニューラルネットワークの矢印も重みを持ちます。入力層から発される矢印の重みを $w$ 、2層から発される矢印の重みを $w'$ とします。

確認のため、上記の $y_1$ のノードを拡大してみましょう。

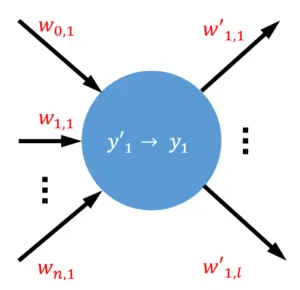
図を拡大すると $y_1$ ノードが入力層から $n + 1$ 個の矢印を受け取り、 $l$ 個の矢印を出力することが分かります。 $n$ 個の入力信号とバイアスから合計 $n + 1$ 個の矢印を受け取ります。

それぞれの重みはどの入力信号を受け取り、どのノードに伝達するかを示します。例えば、重み $w_{1,1}$ は $x_1$ を入力として受け取り、 $y_1$ に伝達しています。

ノードでは以下のように変換が行われています。

$y'_1 = w_{0,1} + w_{1,1} \times x_1 + \ldots + w_{n,1} \times x_n$

$y_1 = \displaystyle \frac{ 1 }{ 1 + \exp ( -y'_1 )}$

活性化関数にはシグモイド関数を用いました。パーセプトロンと同じ計算を行います。

$y_2, y_3, \ \ldots \ , y_m$ も $y_1$ と同じように算出されます。

出力層でも同様の計算が行われます。2層にある $y_1, y_2 , \ \ldots \ , y_m$ を受け取り、重み $w'$ を用いて $z_1, z_2, \ \ldots \ , z_l$ をそれぞれ計算します。

ニューラルネットワークはパーセプトロンを重ねたものと説明しました。では違いはどこにあるのでしょうか。

ニューラルネットワークとパーセプトロンにほとんど違いはありません。パーセプトロンはニューラルネットワークの一種です。

ただ文中に出てくるパーセプトロンは単純パーセプトロンを指すことが多いです。単純パーセプトロンは隠れ層を持たず、活性化関数にステップ関数を用います。

一方でニューラルネットワークは隠れ層を持ち、活性化関数にシグモイド関数やReLU関数などを用いることが一般的です。