活性化関数の役割と代表的な活性化関数～ステップ・シグモイド・ReLU～

活性化関数とは

以下はパーセプトロンのページでも登場した図です。活性化関数は、$y'$を処理する関数$h(y')$のことを指します。

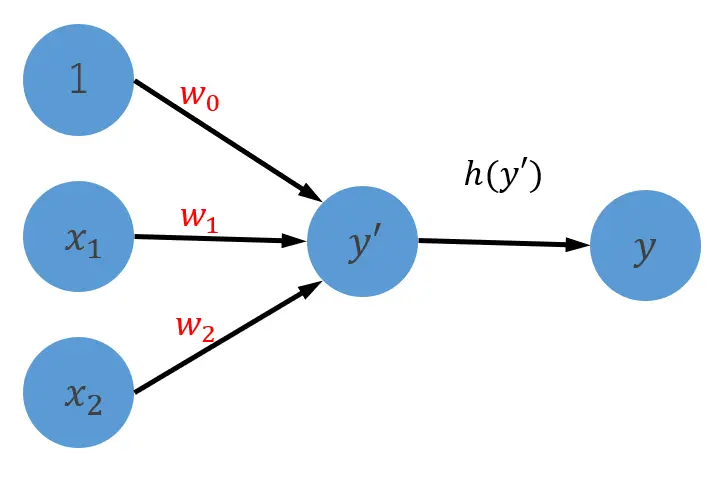
活性化関数を用いるとモデルの表現力が増します。

入力の加重和に対して、活性化関数を用いて変換を行うと様々な値の出力が行えます。様々な値の出力を持つパーセプトロンを組み合わせるとより複雑な表現が可能になります。

以下では、代表的な活性化関数を紹介します。

ステップ関数

ステップ関数は以下の式で表されます。

$$\begin{equation*}\begin{split} h(y') = \begin{cases} 1 & ( y' \geq 0 ) \\ 0 & ( y' \lt 0 ) \end{cases} \end{split}\end{equation*}$$

以下の図を見ると、$y'$の値に応じて階段のようになっていることが分かります。

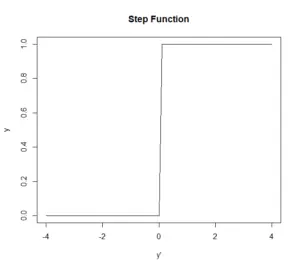
この活性化関数を用いると出力として1と0を得ることができます。

1と0しか出力できないため、情報のロスが激しく表現力に乏しいのが欠点です。

 シグモイド関数

シグモイド関数はニューラルネットワークで用いられる活性化関数ですが、現在はあまり使われていません。

シグモイド関数を活性化関数として用いると勾配消失という現象が起こり、学習が停滞してしまうことがあるためです。

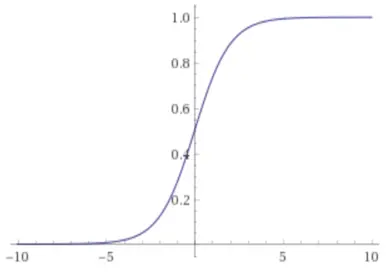
シグモイド関数は以下の数式で表されます。

$h(y') = \displaystyle \frac{ 1 }{ 1 + \exp ( -y' )}$

シグモイド関数を用いると0から1まで連続な値を出力することができます。

$y'$が大きいと出力は1に近づき、$y'$が小さいと出力が0に近づきます。

ReLU関数

ReLU関数は最も一般的に用いられる活性化関数です。勾配消失が起こりにくく、計算しやすいという特徴により、最も活性化関数として使い勝手がいいとされます。

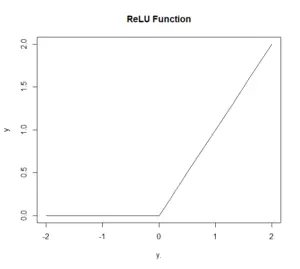
ReLU関数は以下のように表されます。

 $$\begin{equation*}\begin{split} h(y') = \begin{cases} y' & ( y' \geq 0 ) \\ 0 & ( y' \lt 0 ) \end{cases} \end{split}\end{equation*}$$

 また、グラフは以下のようになります。