重回帰分析をわかりやすく解説

回帰分析とは

回帰分析の目的は、目的変数を複数の説明変数を用いて予測、説明することです。

目的変数を予測・分析したいデータ、説明変数をそのために用いるデータと考えるとイメージしやすいです。

例えば、回帰分析を用いることでコンビニの一日の売上を予測、説明することができます。この時、目的変数はコンビニの一日の売り上げ、説明変数には駅からの距離、天気などを用いることができるでしょう。

今回は、重回帰分析理解を深めていきましょう。

重回帰分析とは

重回帰分析では、目的変数に対して複数の説明変数を用います。

身長を目的変数に設定した場合、説明変数に体重、年齢など複数の変数を設定して予測をします。

身長を目的変数 $y$、体重を $x_1$、年齢を $x_2$として、重回帰分析を行うと、次のような式になります。

$y = a_1x_1 + a_2x_2 + b$

単回帰式に説明変数が一つ増えた形になっていますね。このように、重回帰分析では複数の説明変数について考慮したモデルを作成することができます。

重回帰分析では、一般に、目的変数$y$に対して$n$個の説明変数があるときは以下のような形になります。

$y = a_1x_1 + a_2x_2 + \cdots + a_nx_n + b$

この時、$a_i$は$x_i$に対する偏回帰係数と呼びます。

偏回帰係数 $a_i$は、単回帰式と同じように最小二乗法を用いることで求めることができます。

標準化偏回帰係数

重回帰分析において、複数の説明変数の予測力・説明力を比較するときは、標準化偏回帰係数を用います。

この時、偏回帰係数ではなく標準化偏回帰係数を用いるのはなぜでしょうか。

目的変数に対する説明変数の影響度を考えるためには、偏回帰係数に加えてその説明変数の分散を考える必要があります。

どんなに偏回帰係数が大きくても、その説明変数にバラツキがなければ目的変数への影響が少ないと考えられるからです。

具体例として、身長をkgで表された体重、gで表された体重それぞれで単回帰した場合を考えます。

身長に対する体重の影響度は単位によらず同じになるはずですが、回帰係数だけを見て評価すると身長に対する体重の影響度が異なってしまいます。

実際に、身長をkgで表された体重、gで表された体重それぞれで単回帰した結果は以下の通りです。

kgで単回帰：回帰係数0.912

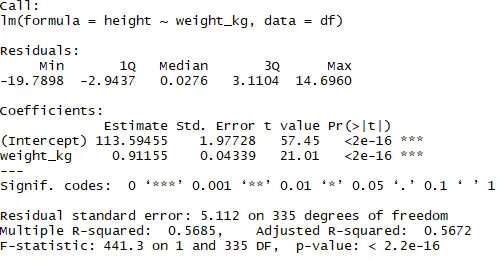
gで単回帰：回帰係数0.000912

回帰係数だけを見て目的変数への影響度を評価すると、kgで表された体重の方が身長への影響が大きいということになります。

これらを標準化偏回帰係数を用いて考えてみましょう。

標準化偏回帰係数を用いることによって、説明変数の分散について考慮することができます。

一般に標準化偏回帰係数$A_i$は、以下のように表されます。目的変数 $y$、説明変数 $x_i$の標準偏差をそれぞれ$s_y$, $s_i$とします。

$A_i = a_i\frac{ s_i }{ s_y }$

この時、kgで表された体重、gで表された体重に対する標準化偏回帰係数$A_kg$、$A_g$は、それぞれ以下のようになります。

$A_{kg} = 0.912*\frac{ 6.426 }{ 7.77 } = 0.754$ 

$A_{g} = 0.000912*\frac{ 6426 }{ 7.77 } =0.754$

身長の標準偏差 $s_y$は、7.77。kg、gで表された体重の標準偏差$s_{kg}$、$s_g$は、6.426、6426を用いました。

$A_i = a_i\frac{ s_i }{ s_y }$

kgで表された体重、gで表された体重どちらも標準化偏回帰係数が0.754になりました。

よって、標準化偏回帰係数を用いると、単位によらず身長に対する体重の影響が同じことがわかります。

ダミー変数

ここまで、身長を体重、年齢から予測する重回帰分析を説明しました。ここに「性別」という説明変数を新たに加えてみましょう。

身長を目的変数 $y$、体重を $x_1$、年齢を $x_2$、性別を $x_3$として、重回帰分析を行うと次のようになります。

$y = a_1x_1 + a_2x_2 + a_3x_3 + b$

ここで、性別という変数をどのようにして重回帰モデルに組み込むかが問題になってきます。

性別は一般に「男性」「女性」などという言葉で表現され、このようなデータのことをカテゴリー変数と呼びます。

一方で、重回帰モデルに組み込む説明変数は数字で表現された数値変数でなくてはなりません。

このようなときに用いるのがダミー変数です。ダミー変数を用いることで、カテゴリー変数を数値変数に変換して重回帰モデルに組み込むことができます。

性別にダミー変数を適用する場合、男を1、女を0のように変換します。

説明変数を選ぶときのポイント

重回帰分析における説明変数選択時のポイントについて説明します。

ポイント1

重回帰分析をする前に、説明変数同士の相関係数を確認しましょう。

説明変数同士の相関が高い（多重共線性がある）とき、偏回帰係数の符号が逆転する、偏回帰係数の有意性が失われるといった問題を引き起こす場合があります。

説明変数同士の相関が高い場合は、その相関が高い説明変数を取り除き一つの変数とするとよいです。

ポイント2

重回帰分析の説明変数の説明力を評価する場合、目的に応じて確認する指標を変える必要があります。

単回帰分析では、モデルの精度の評価に決定係数を用いました。

しかし、重回帰分析では、単純に決定係数のみを用いてモデルの評価をすることはできません。なぜなら、重回帰分析では適当な説明変数を加えることで、決定係数を上げることができるからです。

重回帰分析の説明変数を評価するときは、AIC（赤池情報量基準）を用いることが多いです。

関連記事

線形単回帰分析の仕組みをわかりやすく解説

ロジスティック回帰分析を簡単解説