カイ二乗検定の自由度（分割表の自由度）

二次元分割表の自由度

分割表の自由度は、その分割表を用いて行うカイ二乗検定のカイ二乗統計量の自由度と一致します。つまり、分割表の自由度を求めることはカイ二乗検定においては必須事項です。

自由度とは、変数のうち独立に選べるものの数を指します。

このページでは以下のような二次元分割表を考えます。

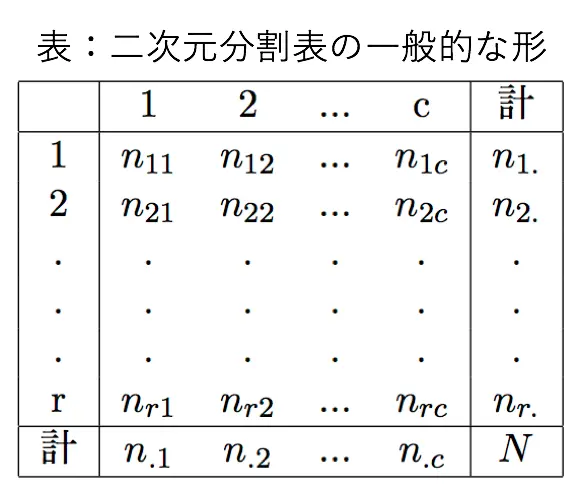
自由度が分かると、どの自由度のカイ二乗分布を用いれば良いかの判断することができます。

自由度の公式は次のようになります。

縦rマス、横cマスの分割表の場合

$自由度 = (r-1)(c-1)$

直観的に考えてみると、分割表の自由度は、周辺合計が計算されたときに、自由に埋めることができる分割表のセル数と考えられます。

周辺合計が分かっているので、縦横とも1行あるいは1列減らした、r-1行、c-1列が自由に決められるセルの行数・列数になります。

よって、自由に決められる、セルの個数はその積で表され、$自由度 = (r-1)(c-1)$となるのです。

数式から自由度を決定する方法

数式から自由度を求めてみましょう。

まず、分割表における独立性の検定のための統計量は次のようになります。

$\chi^2 = \sum^{r}_{i=1}\sum^{c}_{j=1}\frac{(n_{ij}-E_{ij})^2}{E_{ij}}$

ここで、独立であるという帰無仮説が真である場合について、$\chi^2$の分布を近似するカイ二乗分布の自由度を考えることにします。

その自由度は、分割表の行と列の周辺合計が固定されているとすれば、単にカイ二乗統計量の式の独立した項の数といえます。

しかし、これらの項のいくつかは、行と列の合計に関する知識によって決められています。

例えば、$r$個の行の合計を知ることは、それぞれの行において、1つずつ、すなわち度数$n_{ij}$を$r$個固定することになりますので、この式において、$r$個の項は決定されてしまいます。

したがって、独立した項の数は$(rc-r)$個に減少します。

それぞれの行合計によって固定された度数が、$c$個の列合計のうち、最後の列の中にあったとすれば、最初の$(c-1)$個の列合計が、まだ考慮されずに残っているということです。

この列合計の一つ一つが、分割表の度数を一つずつ固定し、その結果として、独立した項の数を減少させます。

よって、独立項としては$rc-r-(c-1)$個が残っていることになります。

つまり、自由度$d.f$（degree of freedom）は次のようになります。

$d.f = rc - r - (c-1) = (r-1)(c-1)$

関連記事

カイ二乗分布のわかりやすいまとめ

独立性のカイ二乗検定を例題を用いてわかりやすく解説