独立性のカイ二乗検定を例題を用いてわかりやすく解説

独立性のカイ二乗検定とは

独立性の検定は、2つの変数に関連が言えるのか否かを判断するためのものです。

帰無仮説$H_0$と対立仮説$H_1$は以下のように定義されます。

$H_0$：二つの変数は独立である
$H_1$：二つの変数は独立ではない（何らかの関連がある）

また、独立の場合、同時確率は掛け算で表せるので、これを数式で表すと次のようになります。

$H_0\ \ \ \ p_{ij} = p_{i.}p_{.j}$
$H_1:not H_0$

これについて仮説検定を行い、p値が有意水準以下になれば、帰無仮説を棄却し対立仮説を採択、つまり2つ変数の間に関連があるといえることになります。

独立性のカイ二乗検定の手順

独立性のカイ二乗検定の基本的な手順は以下のようになります。

1. 2つの変数が独立と仮定すると、各々のセルに入るべき値はこのくらいになるという期待のもと、期待度数を計算。
2. 期待度数と実際の度数の差の二乗を期待度数で割った結果の和を計算。
3. ２の結果は 自由度$(r-1)(c-1)$のカイ二乗分布に従うのでカイ二乗分布表から、p値を発見。（r、ｃはそれぞれ行数、列数。今回の場合、自由度は１）
4. p値が0.05以下なら、帰無仮説を棄却。

独立性のカイ二乗検定の例題

例題に沿って確認していきましょう。

例題

ある病気Aの感染経験について調査したところ、男女別に以下のようなデータが得られました

病気Aの感染経験と性別の間に関連性があると言えるでしょうか？有意水準$α=0.05$として、独立性のカイ二乗検定によって結論づけましょう。

まず、帰無仮説と対立仮説をそれぞれ、以下のように置きます。

帰無仮説$H_0$：性別と病気Aの感染経験は独立である（関連性はない）
対立仮説$H_1$：性別と病気Aの感染経験は独立ではない（何らかの関連性がある）

このとき、帰無仮説の下で分割表の各セルの期待度数を考え、観測度数との差に基づいて検定を行うのが、独立性のカイ二乗検定の基本的な考え方です。

ちなみに、この手法を提唱したピアソンという人の名を取って、ピアソンのカイ二乗検定と呼ばれることもあります。

2つの変数が独立であれば、「各セルに入る数字はこのような値になるだろう」という期待度数を考え、観測データが期待度数と大きく異なっていたとき、「期待と異なるいうことは2つの変数は独立ではない」と結論づけます。

ここで、セル番号($i,j)$の期待度数を$E_{ij}$とし、セル番号($i,j)$の観測度数を$n_{ij}$として、期待とのずれを全セルの観測度数と期待度数の差の二乗を期待度数で割った値の和で定義します。

度数が大きいと近似的に自由度$(r-1)(c-1)$のカイ二乗分布に従うので次のように表せます。

$\\chi^2 = \sum^{r}_{i=1}\sum^{c}_{j=1}\frac{(n_{ij}-E_{ij})^2}{E_{ij}}\ \ \ \ 〜\chi^2((r-1)(c-1))$

ここで$r$と$c$は分割表の縦のセルの個数と横のセルの個数を表しており、自由度が$(r-1)(c-1)$になる理由は、行の和と列の和が固定されているので、その分、列・行それぞれに関して、自由度が1小さくなるからです。

カイ二乗検定の自由度や分割表に関しては「カイ二乗検定の自由度（分割表の自由度）」もご確認ください。

また、検定に用いる推定期待度数$E_{ij}$は以下によって求められます。

$E_{ij} =\frac{n_{i.}n_{.j}}{N}$

さて、今回の問題において、期待度数とカイ二乗統計量は次のようになります。（期待度数の算出法の理論は後述）

$\chi^2 = \frac{(76-61.1)^2}{61.1}+\frac{(42-56.9)^2}{56.9}+\frac{(57-71.9)^2}{71.9}+\frac{(82-67.1)^2}{67.1} = 13.07$

そして、カイ二乗分布表からp値は0.0003と分かるので、帰無仮説が棄却され対立仮説を採択します。

よって、「病気Aの感染経験と性別の間に関連性はある」と言えます。

分割表の二変数が独立と仮定した場合の期待度数

例題のなかで、期待度数は以下によって求められると述べました。ここでは、このように表される理論を説明します。

$E_{ij} =\frac{n_{i.}n_{.j}}{N}$

まず、以下のような分割表を考えます。

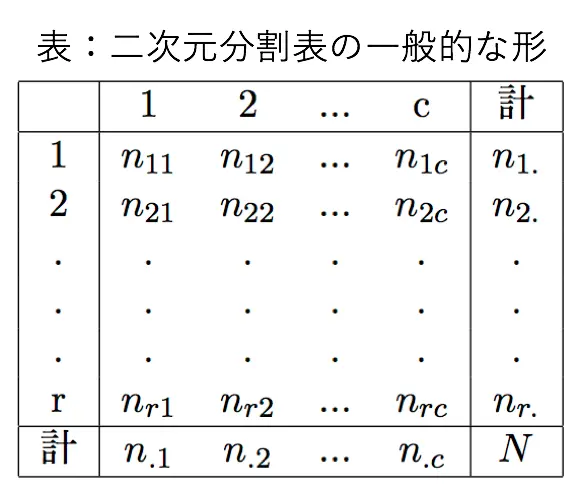
$N$人の標本によって得られる$r \times c$分割表の、$i$行目$j$列目のセルにおける期待度数$F_{ij}$は次のように与えられます。

$F_{ij} = Np_{ij}$

この$F_{ij}$の推定値である$E_{ij}$を求めることが最終目標です。

そこで、$i$行目のカテゴリーに属する観測値の母集団における確率を$p_{i.}$とし、$j$列目のカテゴリーに属する観測値の母集団における確率を$p_{.j}$と置くことにします。

すると、母集団における2変数が独立であるとき、確率の乗法則から次の式が成り立ちます。

$p_{ij} = p_{i.}p_{.j}$

したがって、分割表による期待度数は、次の式によって独立性が示されます。

$F_{ij} = Np_{i.}p_{.j}$

また、$p_{i.}$と$p_{.j}$の最尤推定量$\hat{p_{i.}},\hat{p_{.j}}$は次の式です。

$\hat{p_{i.}} = \frac{n_{i.}}{N} (i =1,...,r)$
$\hat{p_{.j}} = \frac{n_{.j}}{N} (i =1,...,r)$

この最尤推定値を用いて、2つの変数が独立であると仮定した場合、分割表におけるi行目、j列目のセル内の期待度数が、これまでの式により推定可能です。

その推定値$E_{ij}$は次のとおりです。

$E_{ij} = N\hat{p_{i.}}\hat{p_{.j}} = N\frac{n_{i.}}{N}\frac{n_{.j}}{N} = \frac{n_{i.}n_{.j}}{N}$

$(i = 1,...,r, j = 1,...,c)$

カイ二乗検定の自由度

「検定に使うカイ二乗統計量は自由度$(r-1)(c-1)$のカイ二乗分布に従う」ということは先に示した通りですが、これについて補足説明を加えます。

そもそも自由度とは、分割表の自由に決められるセルの数のことです。周辺合計がわかっているので、縦横とも1行あるいは1列減らした、r-1行、c-1列が自由に決められるセルの行数、列数になります。

よって、自由に決められる、セルの個数はその積で次のように表されます。

$自由度 = (r-1)(c-1)$

カイ二乗検定の自由度の詳細は、「カイ二乗検定の自由度（分割表の自由度）」をご確認ください。