カイ二乗検定のわかりやすいまとめ

2024.3.27

カイ二乗検定とは

カイ二乗検定とは帰無仮説が正しいとしたもとで、検定統計量が（近似的に）カイ二乗分布に従うような仮説検定手法の総称です。

代表的なものとして、ピアソンのカイ二乗検定、カイ二乗の尤度非検定、マンテル・ヘンツェルのカイ二乗検定、イェイツのカイ二乗検定などがあります。

独立性のカイ二乗検定は、2つの変数に関連があるかを判断するためのものです。

帰無仮説 $H_0$ と対立仮説 $H_1$ は以下のように定義されます。

$H_0$ ：二つの変数は独立である。
$H_1$ ：二つの変数は独立ではない（何らかの関連がある。）

次のような分割表を考えます。

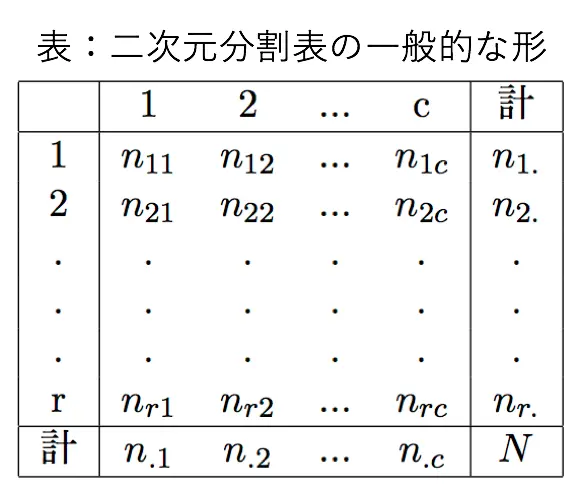
独立ならば同時確率は確率の掛け算で表せることを利用して、先ほど立てた帰無仮説と対立仮説を数式化すると次のようになります。

$H_0\ \ \ \ p_{ij} = p_{i.}p_{.j}$
$H_1:not H_0$

ここで帰無仮説が正しいときに、

$\chi^2 = \sum^{r}_{i=1}\sum^{c}_{j=1}\frac{(n_{ij}-E_{ij})^2}{E_{ij}}\ \ \ \ 〜\chi^2((r-1)(c-1))$

はカイ二乗分布に従うことを利用して行うのが独立性のカイ二乗検定です。

独立性のカイ二乗検定についてさらに詳しく知りたい方は「独立性のカイ二乗検定を例題を用いてわかりやすく解説」をご確認ください。

また、ここでの期待度数の求め方は、「独立性の検定の期待度数の最尤推定量を導出」をご参照ください。

適合度検定(goodness of fit test)とは、帰無仮説における期待度数に対して、実際の観測データの当てはまりの良さを検定するための手法です。

観測度数と期待度数が下の表のようになっているものを考えます。

このとき、カイ二乗の適合度検定は以下のような手順で行われます。

１.期待確率から期待度数を計算
２.カイ二乗値を計算。（これは、観測度数と期待度数の差の二乗を期待度数で割った値の和で計算される。）
３.カイ二乗分布表から、２で計算したカイ二乗値に基づくp値を求める。有意水準以下ならば帰無仮説を棄却。

適合度検定についてさらに詳しく知りたい方は、「適合度の検定をカイ二乗検定で実施する手順を例題でわかりやすく解説」をご確認ください。

独立性のカイ二乗検定を行ない、2つの変数の関連が言えたとします。

このとき分かるのは2つの変数に何らかの関係があるということだけで、具体的にどのような関係があるかはわかりません。

そこで、残差分析によって具体的にどの項目に関連があったのか調べることが重要です。

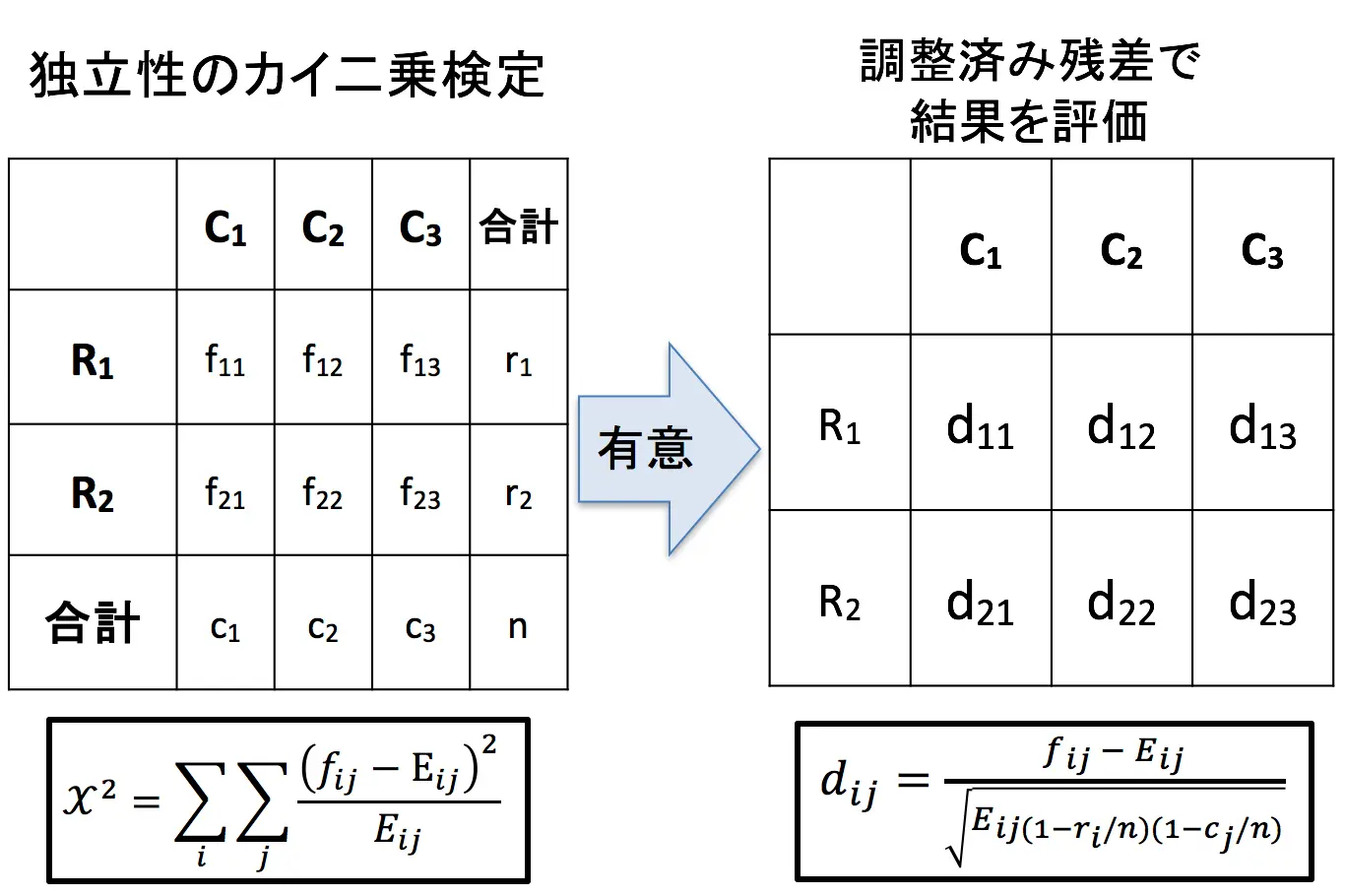
例えば、独立性のカイ二乗検定で独立でない（関連性がある）と言えたとき、調整済み残差 $d_{ij}$ を用いて残差分析を行う図式は以下のようになります。

カイ二乗検定で使う分割表の自由度は、 $自由度 = (r-1)(c-1)$ で与えられます。詳しくは「カイ二乗検定の自由度（分割表の自由度）」をご確認ください。

カテゴリ: 仮説検定