線形単回帰分析の仕組みをわかりやすく解説
このページでは、回帰分析における基本である単回帰分析を用いて回帰分析の理解を深めましょう。
回帰分析とは
回帰分析の目的は、目的変数を複数の説明変数を用いて予測、説明することです。
目的変数を予測・分析したいデータ、説明変数をそのために用いるデータと考えるとイメージしやすいです。
例えば、回帰分析を用いることでコンビニの一日の売上を予測、説明することができます。この時、目的変数はコンビニの一日の売り上げ、説明変数には駅からの距離、天気などを用いることができるでしょう。
今回は、回帰分析のなかで最もシンプルな単回帰分析について考えることで回帰分析への理解を深めていきましょう。
単回帰分析とは
単回帰分析では、目的変数に対して1つの説明変数を用います。
例えばある人の身長を体重から予測したい場合、身長を目的変数、体重を説明変数とします。体重が増えれば、身長も増えるという予測ができます。
身長と体重の例を単回帰分析を用いて考えてみましょう。
身長をと体重をとして以下の式を考えます。
この式の,が分かれば、体重を用いて身長を予測することができます。
この,を回帰係数といいます。
この回帰係数が大きければ大きいほど、目的変数に及ぼす説明変数の影響が大きくなるとわかりますね。
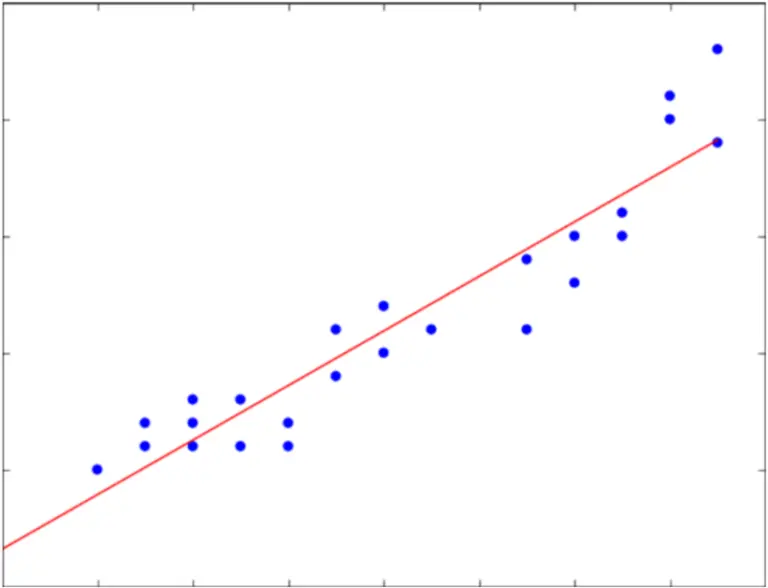
上記の図における青い点は実際のデータを表しています。赤い直線は回帰直線と呼ばれ、回帰式に基づいた予測の集合です。
また単回帰式では、は回帰直線の傾き、は切片を表します。
それでは、,の求め方として、最小二乗法を使った手法を説明します。
最小二乗法を用いた回帰式の導出
最小二乗法では、予測(赤い直線)と実値(青い点)のズレを最小にするための,を求めます。
以下の図におけるとの距離が予測と実際の値のズレです。
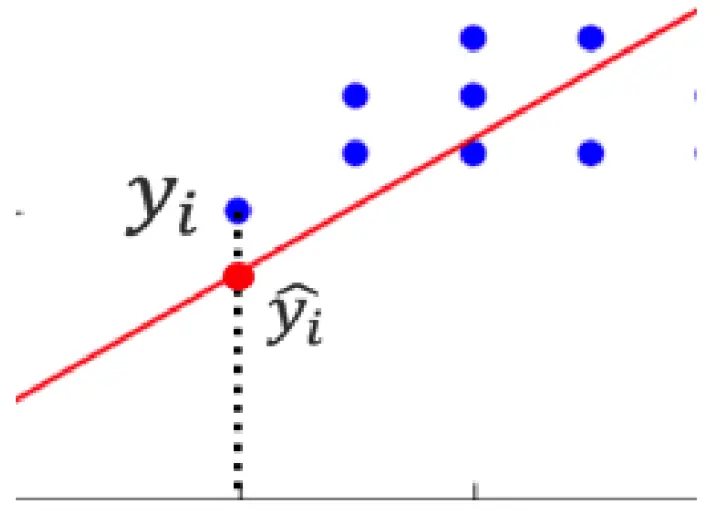
予測と実値の和のことを残差平方和といい、次のように表されます。
最小二乗法では、残差平方和を最小にするための,を求めます。
そのために残差平方和 を,に関して偏微分し、それが0となる,を求めましょう。
に関して偏微分し、を解くと
... ①
に関して偏微分し、を解くと
... ②
と求めることができます。
この二つの①,②に関して連立方程式を解くと、
と求めることができます。
回帰式の評価
回帰係数
回帰分析では、目的変数に対して説明変数が影響を及ぼしているかどうかをP値を用いて判断します。
このP値が0.05より小さいときに説明変数が目的変数に対して影響を及ぼしていると考えられます。
P値が0.05より大きい場合は、「目的変数に対して説明変数が影響を及ぼしていない」という可能性を否定できません。
上記は仮説検定の考え方を用いています。仮説検定については「仮説検定とは?初心者にもわかりやすく解説」をご確認ください。
決定係数
回帰式の予測、説明力を評価するためには決定係数を考えます。
決定係数とは、回帰式でどれだけ目的変数の動きを説明できているかを意味し、次のように表すことができます。
ここで、回帰変動、全変動とします。
回帰変動とは回帰式が予測、説明できている目的変数の動き、全変動とは目的変数の動きを意味します。
決定係数が高ければ高いほど、目的変数の動きを予測、説明できている良いモデルといえます。
関連記事
カテゴリ: 回帰分析
関連するサービス
記事の筆者

AVILEN編集部
株式会社AVILEN





