Σ記号を分かりやすく解説

Σ記号の読み方

Σ記号の読み方は”Σ(シグマ)記号”です。これはギリシャ文字の1つで、現代のアルファベットの「S」に当たる文字です。

シグマ記号の大文字は"Σ"で表記され、小文字は"σ"で表記されます。どちらも数学の分野でよく表記される記号です。

Σ記号の意味

Σ記号はアルファベットの「S」を意味するため、「S」から始まる単語を表記する時によく用いられます。

大文字のΣ記号は合計、総和(Summetion)を意味し、小文字のσ記号は標準偏差(Standard deviation)を意味します。

前述の通りΣ記号とは"総和記号"といって、「1+2+3+4+5+6+...+100」のように繰り返し足し算する時に表記される記号です。

Σ記号には繰り返し足し算する時の条件を示すために添え字が付きます。これが一見難解に見えるのですがルールを押さえると理解しやすくなります。

Σ記号の定義

数学に用いられるΣ記号の定義は次のようになります。

$\sum_{k=1}^{n} a_k=a_1+a_2+a_3+...+a_n$

Σ記号を用いると繰り返し足し算する式をまとめて表記することができます。

添え字の書き方

Σ記号の添え字のルールは以下のようになります。

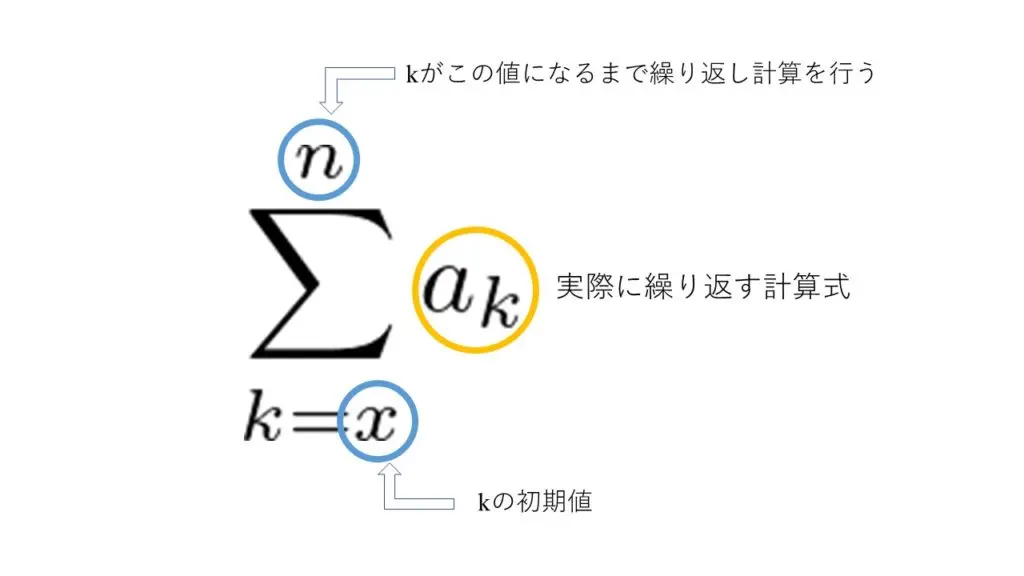
• $a_k$は実際に繰り返す計算式
• $k=x$の値は「kの初期値」
• $n$の値は「$k$がこの値になるまで計算を繰り返す」

例えば$k=1,n=3,a_k=10$の条件の時は

$\sum_{k=1}^{3} 10=10+10+10$

ただ注意すべき点としては、nの値は必ずしも繰り返す回数ではないということです。

例えば$k=3,n=5,a_k=10$の条件の時は

$\sum_{k=3}^{5} 10=10+10+10$

という表記になります。

この時、$n=5$なので10を足す計算を5回繰り返すと思われますが、初期値が3なので$k=3,4,5$となるので、最終的に3回しか繰り返しません。

Σ記号の計算例

Σ記号を用いた簡単な例題に取り組んでみましょう

$(1) \sum_{k=1}^{5} 5　\qquad　(2)\sum_{k=1}^{5} k\qquad　(3)\sum_{k=1}^{3} 3k+2$

【解答】

$(1) 5+5+5+5+5\quad A.25 \qquad (2)1+2+3+4+5\quad A.15 \qquad (3)5+8+11\quad A.24\qquad$

Σ記号の公式

公式を活用すると、Σ記号の計算も簡単に解くことが出来るのでぜひ覚えておきましょう。

$\displaystyle(1) \sum_{k=1}^{n}a=na$

$\displaystyle(2)\sum_{k=1}^{n}k=\frac{1}{2}n(n+1)$

$\displaystyle(3)\sum_{k=1}^{n}k^2=\frac{1}{6}n(n+1)(2n+1)$

$\displaystyle(4)\sum_{k=1}^{n}k^3=\{\frac{1}{2}n(n+1)\}^2$

Σ記号が２つあるときの計算

Σ記号が２つあるときとは、以下のような形です。

$\displaystyle\sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}$

Σ記号が2つあるときは、内側のΣ記号から計算していきましょう。

【例題】

$\displaystyle\sum_{i=1}^{5}\sum_{j=1}^{3}2ij$

まず、Σ記号の性質通り内側のΣ記号である$\displaystyle\sum_{j=1}^{3}2ij$から計算していきましょう。

今は$i$は関係ないのでΣ記号の外に出しておきます。

$\displaystyle\sum_{i=1}^{5}i\sum_{j=1}^{3}2j$

Σ記号の公式に従って解くと

$\displaystyle\sum_{j=1}^{3}2j=2\times\frac{1}{2}\times3\times(3+1)$

$\quad\qquad = 12$

よって

$\displaystyle\sum_{i=1}^{5}12i$

これを計算すると

$\displaystyle\sum_{i=1}^{5}12i = 12\times\frac{1}{2}\times5\times(5+1)$

$\qquad\quad = 180$