勾配法の仕組みをわかりやすく解説

勾配法とは

ニューラルネットワークの精度を高めるには、損失関数を最小（予測誤差を最小）にする「最適な重み」を見つける必要があります。

重みの探索には勾配法を用いるのが一般的です。

配法は最小値や最大値を求めるためのアルゴリズムで、解析的に解くことが困難な問題に用いられます。「解析的に解けない」とは、ある関数に対してうまく微分ができない状態を指します。

勾配法の仕組み

勾配法は、関数$f(x)$を最小にする$x$の値、関数$g(x,y,z)$を最小にする$x, y, z$の値の組み合わせといったように、関数を最小にするような変数の値を求めます。

勾配法は傾きが0となる地点$x$が関数の最小、最大値を与えるという考え方に基づいた手法です。これは、傾きが0となる地点で最小、最大値、極小、極大値をとる微分法の考え方に似ています。

勾配法では、数値微分を用いて、傾きが0となる最適な$x$を求めます。具体的な手順は以下の通りです。

1. 初期探索地点$x$を定める。
2. ある地点$x$での傾きを求める。
3. 傾きと学習率をもとに次の探索地点$x'$を求める。
4. 2~3の更新を傾きが0となる$x$が見つかるまで繰り返す。

勾配法と学習率

一変数関数の最小値問題を例に考えてみましょう。

例題

$y = x^2 + 1$という関数について勾配法を用いて最小値を与える$x$を求めましょう。

$y = x^2 + 1$のグラフは以下のようになります。

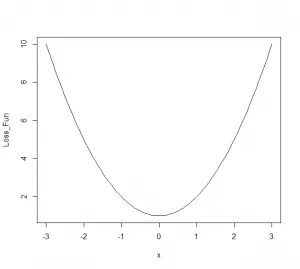
微分法を用いると$y' = 2x$より$x = 0$の時に最小値をとります。

今回は$y = x^2 + 1$について勾配法を用いて、$y$を最小とするような$x$を求めます。

$x_0 = 2$から更新してみましょう。学習率$\eta$は0.25、$f'(x) = 2x$です。

 $x_1 = x_0 - \eta f'(x_0) = 1$

$x_2 = x_1 - \eta f'(x_1) = 0.5$

$x_3 = x_2 - \eta f'(x_2) = 0.25$

$x_4 = x_3 - \eta f'(x_3) = 0.125$

勾配法による更新を続けるとゆっくり$x = 0$に近づき、更新を続けると$x = 0$と求めることができます。

初期値を$x_0 = 2$としましたが、この初期値は自由に設定することができます。

学習率を0.25としました。これも自由に設定することができ、この学習率の値によって学習速度が変化します。

学習率$\eta$が学習速度にどう影響するかを以下のグラフを見て観察してみましょう。

上から順に$\eta = 0.01,\eta = 0.1,\eta = 0.2$とします。

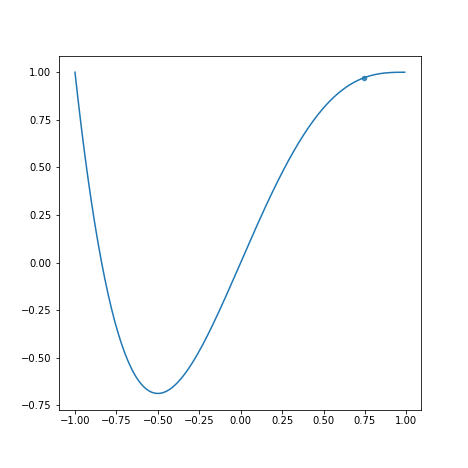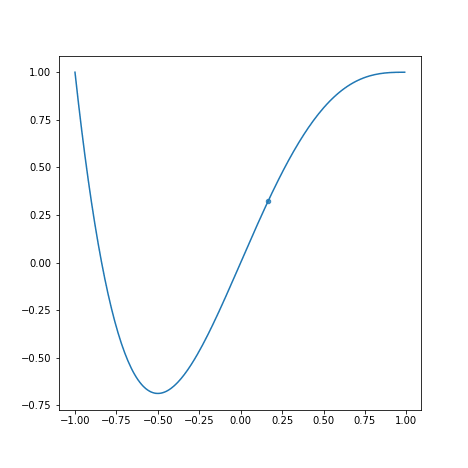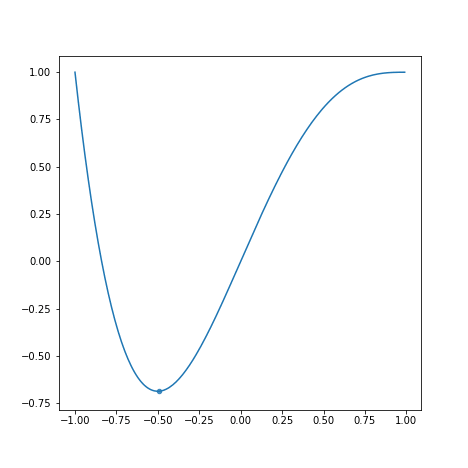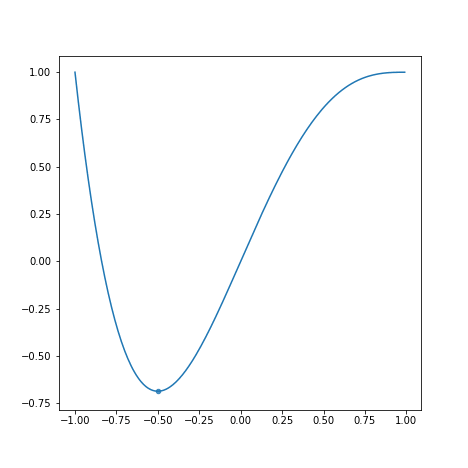
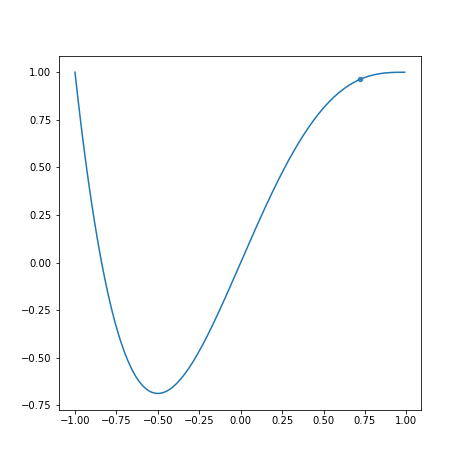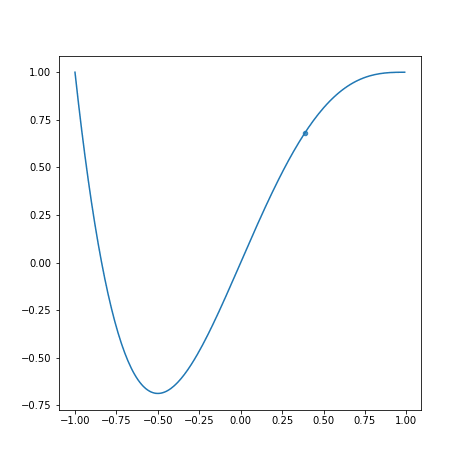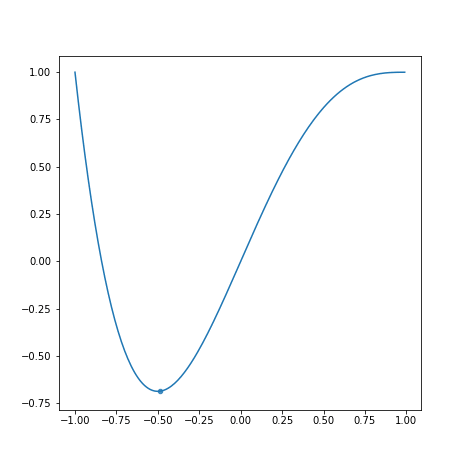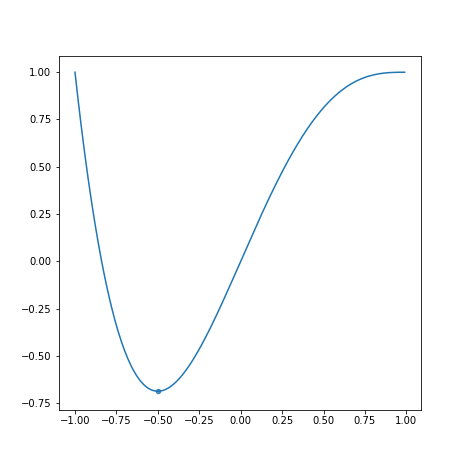
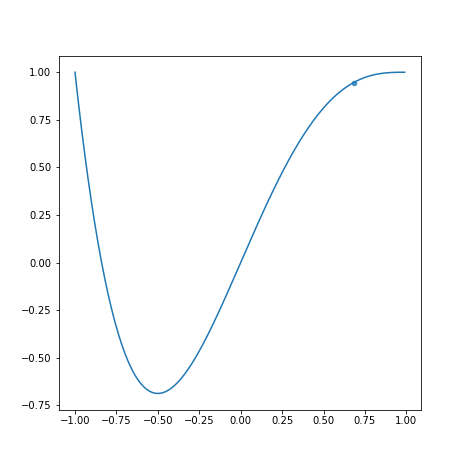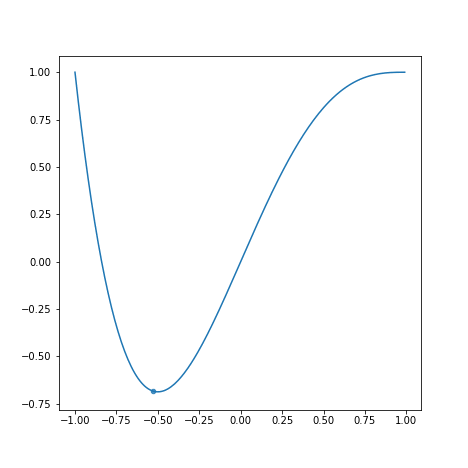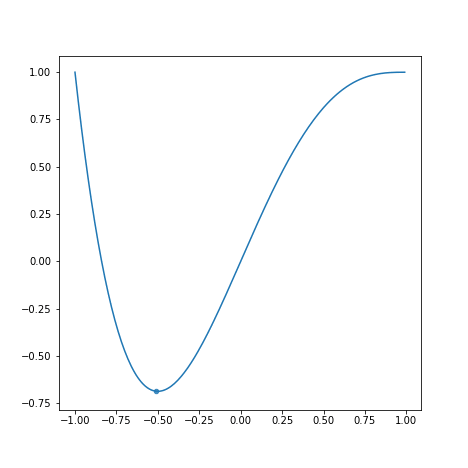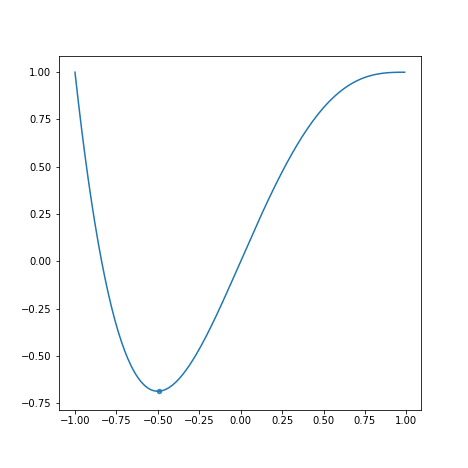
学習率が小さすぎると学習に時間がかかります。また、学習率が大きすぎると最適な値を求めるのにかえって時間がかかっています。

勾配法の一般化

今までは一変数関数について勾配法を用いていました。

変数が増えても勾配法を使うことができます。$n$個の変数を持つ関数についても勾配法を用いることができます。

$n$個の変数を$x_1, \ldots, x_n$とする。

1 初期探索地点$x = (x_1,\ldots, x_n)$ を定める。

2 $x = (x_1,\ldots, x_n)$における勾配を求める。

3 新たに探索する$x' = (x'_1,\ldots, x'_n)$を傾きと学習率$\eta$を用いて求める。更新は以下のように表されます。

$(x'_1, \ldots , x'_n )=x_1 - \eta \frac{ \partial f }{ \partial x_1 } , \ldots , x_n - \eta \frac{ \partial f }{ \partial x_n }$

4 勾配が0となる$x$を見つけるまで2~3の更新を繰り返す。

 勾配の要素がすべて0となるまで更新を続けます。最終的に$x_{final} = (x_1, \ldots, x_n)$が最適な値となります。