無情報事前分布とは

無情報事前分布とは

無情報事前分布とは、事前に情報がない場合に使用される事前分布です。

ベイズ統計では、自分でデータを得る前に、事前の情報から与えられる分布（事前分布）を設定する必要があります。

• 以下の例を考えてみます。

コインを5回投げて4回表が出た。表が出る真の確率pの事後分布を求めよ。

文章の中には事前の情報がありません。

コインの表が出る回数が二項分布に従うことから、共役事前分布であるベータ分布に設定するのもいいですが、$Beta(1/2,1/2)$なのか、$Beta(1,1)$なのか、$Beta(1,2)$なのか、選択肢がたくさんあります。仮に$Beta(1,2)$に設定したとしても、その根拠がなければ信用性に欠けます。

そこで考えられたのが無情報事前分布です。無情報事前分布は、事前に情報がない場合や、事前分布を設定するにあたる根拠がない場合に使用される分布です。

無情報事前分布は主に以下の分布が使われます。

・一様分布
・非正則な分布

これらを使用することにより、「事前に情報がないから事前分布を無情報事前分布に設定した」という根拠が得られます。

無情報事前分布に一様分布を採用する場合

連続一様分布の確率密度関数は以下のように与えられます。

$f(x)=\frac{1}{b-a}\ \ \ \ \ (a\leq x\leq b)$

これを事前分布$\pi(\theta)$に割り当てると、次のように書き換えることができます。

$\pi(\theta)=\frac{1}{b-a}\ \ \ \ \ (a\leq \theta\leq b)$

これをグラフにすると以下のようになります。

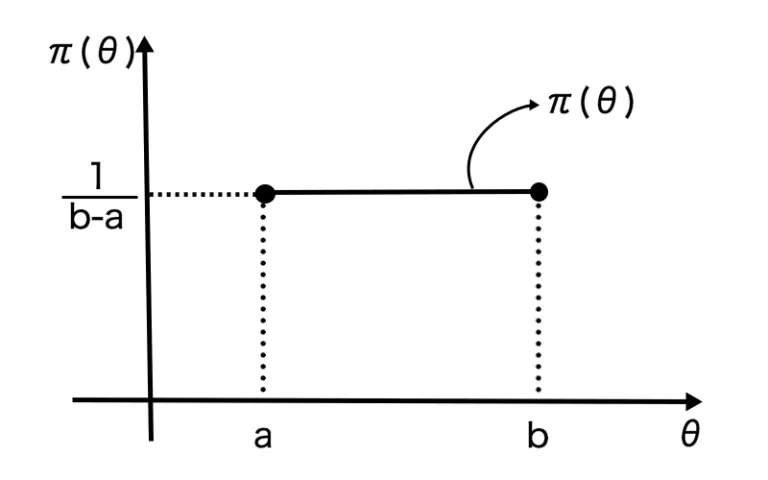
これは閉区間[a,b]の間ではどんな値をとっても全て同じ確率であることを意味しています。

こういった意味で一様分布は無情報分布であるということが言えます。

一様分布を分布とする問題点

一様分布を上記のコインの例題に当てはめると、真の確率pは0から1を取るので、一様分布の事前分布は以下となります。

$\pi(p)=1\ \ \ \ \ (0\leq p\leq 1)$

つまり、表が出る確率が0から1の間でどれも等しいということを意味しています。

見た目が普通のコインならば、表が出る確率が0である確率よりも、$\frac{1}{2}$である確率の方が大きいはずですが、全てが同じ確率であるとして設定してしまっており、一様分布が適していないように見えます。

非正則事前分布とは

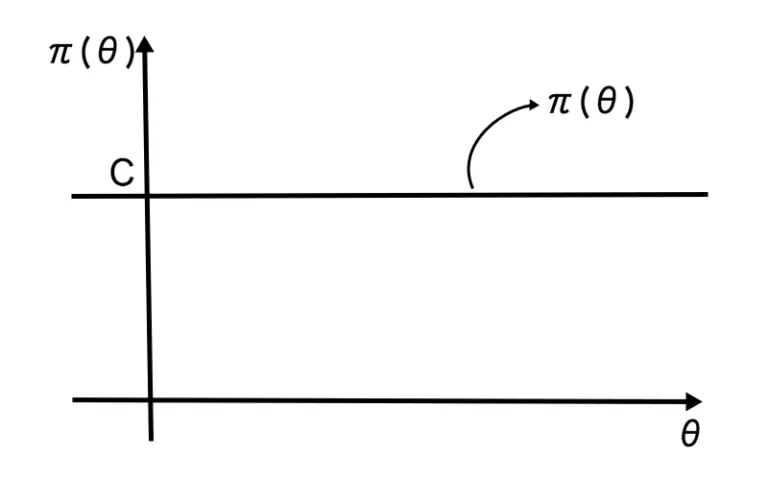
非正則な分布を事前分布に設定したとき、その事前分布を非正則事前分布と言います。

ざっくりいうと一様分布を無限に広げたような形になります。