独立性の検定の期待度数の最尤推定量を導出

期待度数の最尤推定量

独立性の検定において、以下のような二次元分割表を用いる場合を考えます。

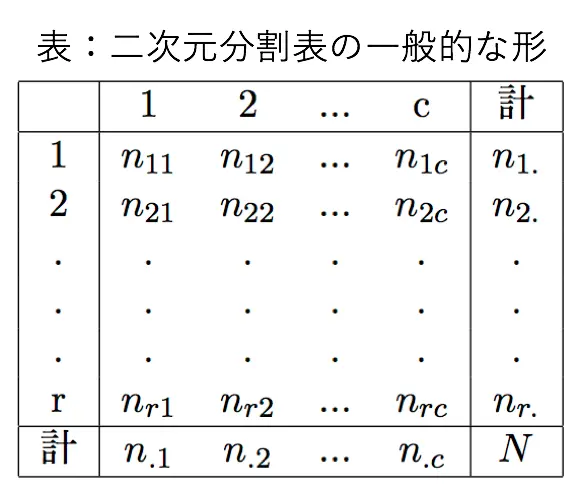
このとき、期待度数の最尤推定量は次の式で表されます。

$E_{ij} = \frac{n_{i.}n_{.j}}{N}$

以降では、上記の式の導出過程を解説します。

期待度数の最尤推定量の導出

一般的なr×c分割表を仮定した場合の最尤推定量を考えます。

分割表の各セルにおける期待度数は最尤推定量によって推定できます。

まずは、$p_{i.}$と$p_{.j}$の最尤推定量$\hat{p_{i.}}$と$\hat{p_{.j}}$を導出します。

ここで、観測度数$n_{ij}$は確率$p_{ij}$で多項分布に従うので、以下のように表されます。

$P(X_{ij}=n_{ij}) = \frac{N!}{\prod_{i=1}^{c}\prod_{j=1}^{r}n_{ij}!}\prod_{j=1}^{c}\prod_{j=1}^{r}p_{ij}^{n_{ij}}$

上式の両辺の対数尤度を求めると、次のようになります。

$logL = log\frac{N!}{\prod_{i=1}^{c}\prod_{j=1}^{r}n_{ij}!}\prod_{j=1}^{c}\prod_{j=1}^{r}p_{ij}^{n_{ij}} = C + \sum_{i=1}^{c}\sum_{j=1}^{r}n_{ij}logp_{ij}$

この条件のもとで、$logL$を最大にする$p_{i.}$と$p_{.j}$を求めます。

ラグランジュの未定乗数法により以下が言えます。

$L^{\ast} = C+ \sum_{i=1}^{c}\sum_{j=1}^{r}n_{ij}logp_{ij} - \phi_{1}(\sum_{i}^{c}p_{i.}-1)-\phi_{2}(\sum_{j}^{r}p_{.j}-1) = C+ \sum_{i=1}^{c}n_{i.}logp_{i.}+ \sum_{j=1}^{r}n_{.j}logp_{.j} - \phi_{1}(\sum_{i}^{c}p_{i.}-1)- \phi_{2}(\sum_{j}^{r}p_{.j}-1)$

よって、以下の式から最尤推定量を求めることができます。

$\frac{\partial L^{\ast}}{\partial p_{i.}} = \frac{n{i.}}{p_{i.}}-\phi_1(\equiv0)$
$\frac{\partial L^{\ast}}{\partial p_{.j}} = \frac{n{.j}}{p_{.j}}-\phi_2(\equiv0)$

したがって、

$n_{i.} - \phi_1p_{i.} = 0$
$n_{.j} - \phi_2p_{.j} = 0$

ここで上式の和をとると、$\phi_1=\phi_2=N$です。

これを、1個前の式に代入して整理すると、$p_{i.}$と$p_{.j}$の最尤推定量$\hat{p_{i.}}$と$\hat{p_{.j}}$は、それぞれ次の式になります。

$\hat{p_{i.}} = \frac{n_{i.}}{N} (i = 1,2,...,r)$
$\hat{p_{.j}} = \frac{n_{.j}}{N} (j = 1,2,...,r)$

したがって、2つの変数が独立であると仮定した場合は、分割表における$ij$セル内の推定期待度数$E_{ij}$が推定でき、それは下式になります。

$E_{ij} = \frac{n_{i.}n_{.j}}{N}$

この期待度数を用いて、独立性の検定を行うことになります。

関連記事

独立性のカイ二乗検定を例題を用いてわかりやすく解説