非正則事前分布とは

非正則事前分布とは

事前分布を非正則な分布に設定したとき、その事前分布を非正則事前分布といいます。非正則事前分布は、ベイズ統計における無情報事前分布のひとつです。

一様分布と非正則分布の比較

非正則な分布は一様分布と非常に似ています。

まず、連続一様分布の確率密度関数は以下のように与えられています。

$f(x)=\frac{1}{b-a}\ \ \ \ \ (a\leq x\leq b)$ 

これをパラメータ$\theta$の事前分布に設定すると以下のように表されます。

$\pi(\theta)=\frac{1}{b-a}\ \ \ \ \ (a\leq\theta\leq b)$ 

この一様分布の確率密度関数のグラフは下図です。

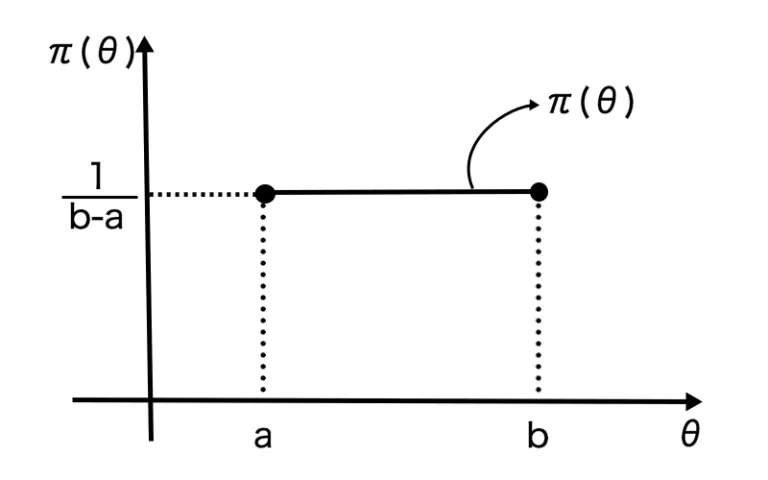
これに対し、非正則な分布の密度関数は、例えば以下 のように与えられます。

$f(x)=C\ \ \ \ \ (-\infty\leq x\leq\infty)$ 

これをパラメータ$\theta$の事前分布に設定すると、

$\pi(\theta)=C\ \ \ \ \ (-\infty\leq\theta\leq\infty)$ 

と表せられます。この非正則な分布の密度関数のグラフは下図です。

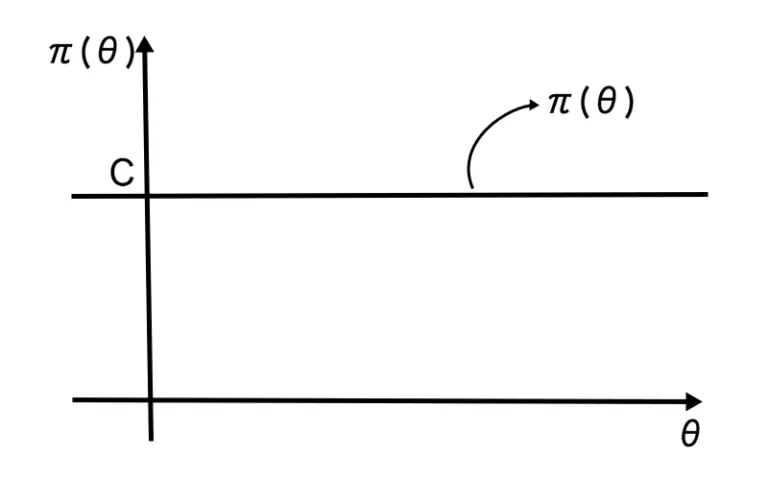
つまり、非正則な分布とは一様分布の範囲を無限に広げた分布のことです。

非正則分布は確率分布ではない

非正則な分布は、よく見てみると確率の和が1ではありません。

数式で表現してみましょう。事前分布をパラメータの取りうる区間で積分すると、

$\int_{\theta\in\Theta}f(x)dx=\int_{-\infty}^{\infty}Cdx=\infty$

となり、積分値が無限大に発散してしまいます。これは、全事象の確率は1であるというコルモゴロフの確率の公理に反しています。

よって、厳密には非正則な分布は確率密度関数ではありません。

非正則事前分布は完全なる無情報事前分布である

それでも非正則な分布が事前分布として使われる理由は、事前分布として機能する上で有用な特徴があるからです。

正規分布を例に、この特徴を考えましょう。

例題

平均$\mu$、分散$\sigma^2$（既知）の正規母集団からデータをn個取ってきた。このときの事後分布とその平均、分散を求めよ。ただし、事前に情報がないため、事前分布を$\pi(\mu)=C\ \ \ \ \ (-\infty\leq\mu\leq\infty)$ と設定する。

標本平均を$\bar{x}$とすると、ベイズの定理より

$\pi(\mu|x)\propto\pi(\mu)f(x|\mu)$

※この式変形は、「正規分布の事後分布の平均と分散」を参照してください。

$\propto C\cdot(\frac{1}{\sqrt{2\pi}\sigma})^nexp[-\frac{1}{2\sigma^2}\{n(\mu-\overline{x})^2+nS^2)\}]$

$C\cdot(\frac{1}{\sqrt{2\pi}\sigma})^n$と$exp[-\frac{nS^2}{2\sigma^2}]$は定数とみなせるので、

$\propto exp[-\frac{n(\mu-\overline{x})^2)}{2\sigma^2}]$

ここに全区間の積分値を1にするための定数（基格化定数）をかけると、

$\pi(\mu|x)=\frac{1}{\sqrt{2\pi\sigma^2/n}}exp[-\frac{n(\mu-\overline{x})^2)}{2\sigma^2}]$

という事後分布が得られます。

この分布の形から、平均と分散が以下となることが分かります。

平均：$\bar{x}$

分散：$\frac{\sigma^2}{n}$

この平均と分散は、サンプルサイズが$n$のときの標本平均と標本分散に一致しています。

つまり、事前分布を非正則な分布に設定すると、事前の情報が一切加味されず、データの情報だけで事後分布が構成されるというわけです。このことから、非正則事前分布は完全なる無情報事前分布として考えられます。

関連情報

無情報事前分布とは

共役事前分布を分かりやすく解説

正規分布の事後分布の平均と分散