掃き出し法を用いた連立一次方程式の解き方を例題で解説

掃き出し法を用いた連立１次方程式の解法

解法の流れは以下のようになります。

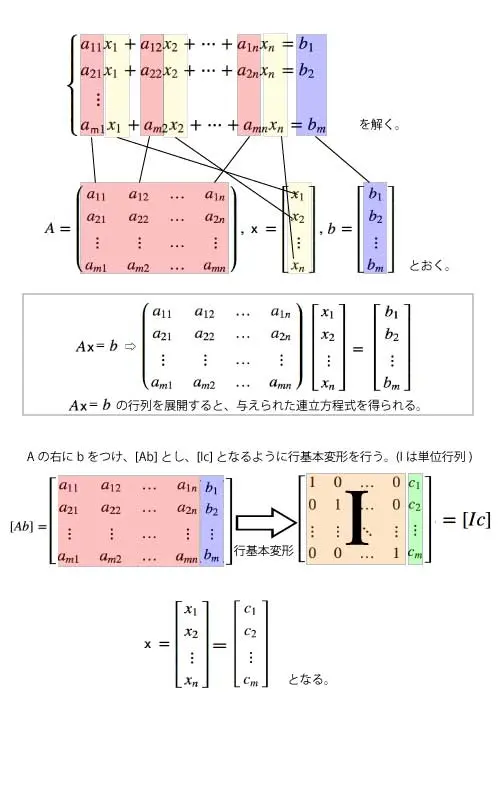
掃き出し法を用いた連立１次方程式の解法

$$\begin{equation*}\begin{split} \left\{ \begin{array}{l} a_{11}x_{1} + a_{12}x_{2} +\cdots + a_{1n}x_{n} = b_{1} \\ a_{21}x_{1} + a_{22}x_{2} +\cdots + a_{2n}x_{n} = b_{2}\\\ \ \ \vdots \nonumber \\ a_{ｍ1}x_{1} + a_{m2}x_{2} +\cdots + a_{mn}x_{n} = b_{m} \end{array} \right. \end{split}\end{equation*}$$

ここで

$\boldsymbol{A} = \left( \begin{array}{cccc} a_{11} & a_{12} & \ldots & a_{1n} \\ a_{21} & a_{22} & \ldots& a_{2n} \\ \vdots & \vdots & \ldots & \vdots \\ a_{m1} & a_{m2} & \ldots & a_{mn} \end{array}\right) , \boldsymbol{x} = \left[ \begin{array}{cccc} x_{1} \\x_{2}\\\vdots\\x_{n} \end{array}\right] , \boldsymbol{B} = \left[ \begin{array}{cccc} b_{1} \\b_{2}\\\vdots\\b_{m} \end{array}\right]$

のように置くと連立方程式を$\boldsymbol{Ax}=\boldsymbol{b}$と書き表すことができ、[$\boldsymbol{Ab}$]を行基本変形し[$\boldsymbol{Ic}$]となるように行基本変形する。 ここで生成された$\boldsymbol{c}$が解$\boldsymbol{x}$となる。

図で解説すると以下の通りです。

例題

それでは、実際に掃き出し法を用いて連立一次方程式を解いてみましょう。

例題

次の連立一次方程式を掃き出し法を用いて求めよ

$$\begin{equation*}\begin{split} \left\{ \begin{array}{l} 2x + 4y + z = 6 \\ x - 2y - 2z = 1 \\ -2x - 5y + 3z = 5 \end{array} \right. \end{split}\end{equation*}$$

解答は以下の通りです。

$\boldsymbol{A} = \left( \begin{array}{cccc}2&4&1\\1&-2&-2\\-2&-5&3\end{array}\right)$

$\boldsymbol{x} = \left( \begin{array}{cccc}x\\y\\z\end{array}\right)$

$\boldsymbol{b} = \left( \begin{array}{cccc}6\\1\\5\end{array}\right)$

$[Ab]=\left( \begin{array}{cccc}2&4&1&6\\1&-2&-2&1\\-2&-5&3&5\end{array}\right)$

1行目を3行目に足します。

$→\left( \begin{array}{cccc}2&4&1&6\\1&-2&-2&1\\0&-1&4&11\end{array}\right)$

1行目を2行目にを交換します。

$→\left( \begin{array}{cccc}1&-2&-2&1\\2&4&1&6\\0&-1&4&11\end{array}\right)$

1行目を-2倍し、2行目に足します。

$→\left( \begin{array}{cccc}1&-2&-2&1\\0&8&5&4\\0&-1&4&11\end{array}\right)$

3行目を８倍し、2行目に足します。

$→\left( \begin{array}{cccc}1&-2&-2&1\\0&0&37&92\\0&-1&4&11\end{array}\right)$

2行目と3行目を入れ替えます。

$→\left( \begin{array}{cccc}1&-2&-2&1\\0&-1&4&11\\0&0&37&92\end{array}\right)$

２行目を-1倍し、３行目を$\frac{1}{37}$倍します。

$→\left( \begin{array}{cccc}1&-2&-2&1\\0&1&-4&-11\\0&0&1&\frac{92}{37}\end{array}\right)$

このように対角成分を１、下三角成分を０にすることを前進消去と呼びます。

次に、上三角成分を0にする、後退代入を行います。

3行目を4倍して2行目に足します。

$→\left( \begin{array}{cccc}1&-2&-2&1\\0&1&0&-\frac{39}{37}\\0&0&1&\frac{92}{37}\end{array}\right)$

2行目、3行目をそれぞれ2倍し、1行目に足します。

$→\left( \begin{array}{cccc}1&0&0&\frac{143}{37}\\0&1&0&-\frac{39}{37}\\0&0&1&\frac{92}{37}\end{array}\right)$

よって、解$\boldsymbol{x}$は、

$\boldsymbol{x}=\left( \begin{array}{cccc}x\\y\\z\end{array}\right)=\left(\begin{array}{cccc}\frac{143}{37}\\-\frac{39}{37}\\\frac{92}{37}\end{array}\right)$