余因子・余因子行列の求め方を例題で解説

余因子とは

余因子の定義は以下の通りです。

余因子の定義

正方行列$Aに$対して、Aの第$i$行と第$j$列を取り除いた行列を$A_{ij}$とすると、以下となる。

$\tilde{ a } = (-1)^{i+j}|A_{ij}|$

ことのき$\tilde{ a }$をAの$(i,j)$余因子とよぶ。

余因子のイメージは以下の図のようになります。

それでは、例題で余因子を求めてみましょう。

例題

行列$A =\begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9  \end{pmatrix}$のとき、$(2,2)$余因子と$(2,3)$余因子を求めよ。

解答は以下の通りです。

$(2,2)$余因子は行列$A$の第2行と第2列を取り除くので、

$\tilde{ a }_{22}  =  (-1)^{2+2}\begin{vmatrix} 1 & 3 \\ 7 & 9   \end{vmatrix}$

$= -12$

同様に$(2,3)$余因子は、

$\tilde{ a }_{23}  = (-1)^{2+3}\begin{vmatrix} 1 & 2 \\ 7 & 8    \end{vmatrix}$

$=6$

余因子行列とは

余因子行列の定義は以下の通りです。

余因子行列の定義

正方行列$A$の$(i,j)$余因子をすべて求め、行列にした後、転置した行列が余因子行列である。

余因子行列のイメージは以下の図のようになります。

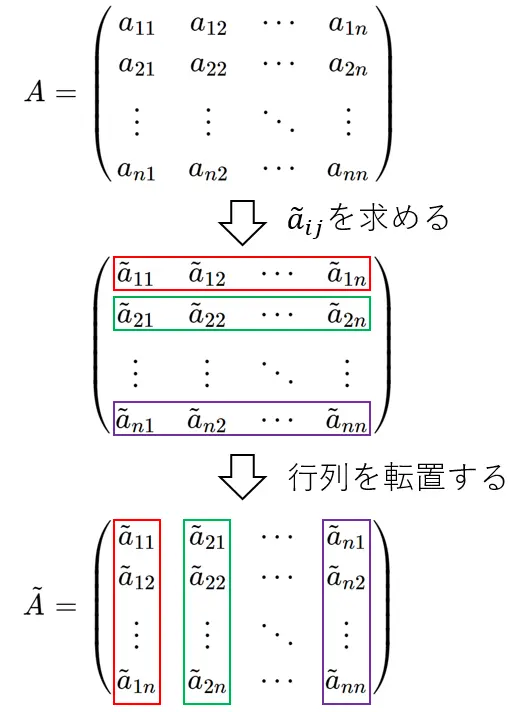
それでは、例題で余因子行列を求めてみましょう。

例題

列$A =  \begin{pmatrix} 2 & 1 & 3 \\ 1 & -2 &-2 \\ 2 & -1 & -1 \end{pmatrix}$のとき、余因子行列$\tilde{ A }$を求めよ。

解答は以下の通りです。

上記を転置して、

$\tilde{ A } =\begin{pmatrix} 0 & -4 & 8 \\ -3 & -8 & 7 \\ 3 & 0& -3\end{pmatrix}$となります。