カイ二乗分布のわかりやすいまとめ

2024.3.17

2024.3.28

カイ二乗分布

このページでは、カイ二乗分布に関する特徴をまとめて紹介します。

カイ二乗分布とは
カイ二乗分布のグラフ
カイ二乗分布の積率母関数
カイ二乗分布の確率密度関数
カイ二乗分布の期待値と分散
カイ二乗分布の性質
カイ二乗分布とF分布の関係
カイ二乗分布とt分布の関係
カイ二乗分布を用いた検定（カイ二乗検定）
関連記事

カイ二乗分布とは

確率変数 $Z_1,Z_2,...,Z_n$ が互いに独立であり、それぞれが標準正規分布 $N(0,1)$ に従うとき、

$χ^2 = Z^2_1 + Z^2_2 +,...,+Z^2_k$

の $χ^2$ に従う分布を、自由度 $k$ （足される標準正規分布の数）のカイ二乗分布といいます。

※ $χ$ はギリシャ文字であり、カイと読みます。アルファベットのエックス（X）ではないことに注意

カイ二乗分布のグラフ

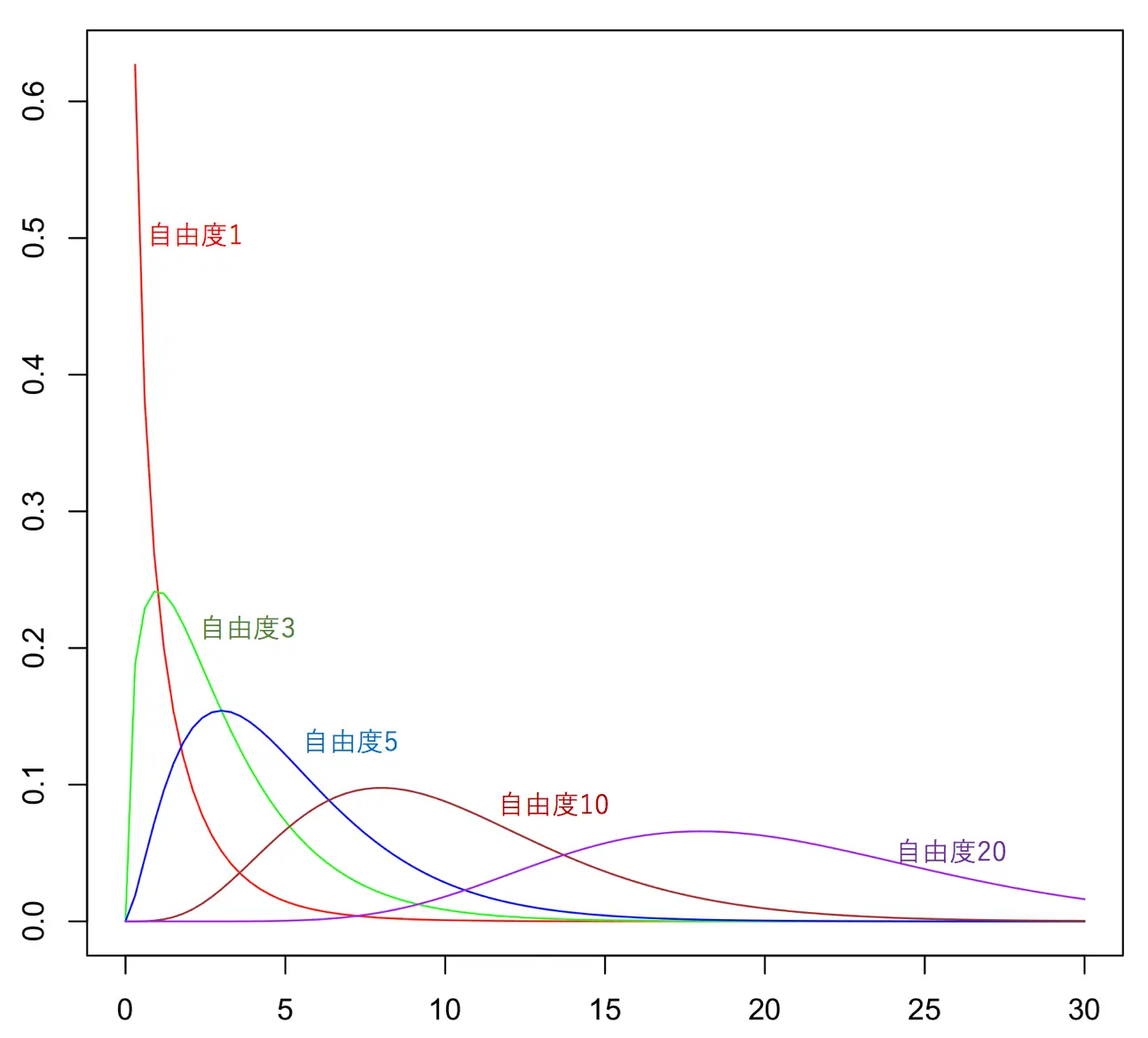
カイ二乗分布のグラフは以下のようになります。

カイ二乗のグラフは自由度によって大きく形状が異なります。これは、カイ二乗分布の自由度が、足される独立な標準正規分布の個数によって決まることに起因します。

カイ二乗分布の積率母関数

カイ二乗分布の積率母関数は以下となります。

$M_{X}(t)={(\frac{1}{1- 2 t})}^{\frac{k}{2}}$

導出に関しては、「積率母関数を用いたカイ二乗分布の期待値と分散の導出」をご確認ください。

カイ二乗分布の確率密度関数

自由度 $n$ のカイ二乗分布の確率密度関数は以下となります。

$f(χ) = \frac{1}{2^\frac{n}{2}Γ(\frac{n}{2})}(χ^2)^{\frac{n}{2}-1}e^{-\frac{χ^2}{2}}$

ただし、 $Γ(\frac{n}{2})$ はガンマ関数であり、

$Γ(\frac{n}{2}) = \int_0^∞ t^{\frac{n}{2}-1}e^{-t} dt$

です。

カイ二乗分布の期待値と分散

カイ二乗分布の期待値と分散は以下となります。

期待値	$E(x)=k$
分散	$V(x)=2k$

積率母関数を用いた導出は「積率母関数を用いたカイ二乗分布の期待値と分散の導出」をご確認ください。

確率密度関数を用いた導出は「確率密度関数を用いたカイ二乗分布の期待値と分散の導出」をご確認ください。

カイ二乗分布の性質

カイ２乗分布には2つの性質があります。

性質1
二つの確率変数 $W_1,W_2$ が、互いに独立に $χ^2(n_1),χ^2(n_2)$ に従うとき、確率変数の和 $W1+W2$ もまたカイ二乗分布に従い、その自由度は $n_1+n_2$ である。
これをカイ二乗分布の再生性といいます

性質2
$N(μ,σ^2)$ の正規分布に従う母集団より抽出された、大きさ $n$ の無作為標本 $X_1,X_2,...,X_n$ において、それぞれの $X$ は互いに独立に正規分布に従うので、
$W = \sum_{ i = 1 }^{ n } \frac{(X_i-\bar{X})^2}{σ^2} = \frac{(n-1)S^2}{σ^2}$
の $W$ は自由度n-1のカイ二乗分布に従う。

カイ二乗分布とF分布の関係

F分布とは以下のような分布で、カイ二乗分布と親密な関係があります。

$X$ と $Y$ が互いに独立である確率変数 $X, Y$ について、 $X$ が自由度 $n$ のカイ二乗分布、確率変数 $Y$ が自由度 $m$ のカイ二乗分布に従うと仮定します。
このとき、
$F = \frac{\frac{X}{n}}{\frac{Y}{m}}$
と表される $F$ が従う分布を、F分布という。