カイ二乗検定を残差分析で評価する方法

残渣分析とは

分割表を用いた独立性のカイ二乗検定で2つの変数の間に関連がある分かったとき、変数の間にある具体的な関係を評価するのが残差分析です。

残差は「観測値$-$期待値」で算出します。

残差分析を行うことで期待度数と観測値のずれが特に大きかったセルを発見することができます。

調整済み残差を用いたカイ二乗検定の残差分析

独立性のカイ二乗検定で2つの変数が独立でない（関連性がある）と言えたとき、調整済み残差$d_{ij}$を用いて残差分析を行う図式は以下のようになります。

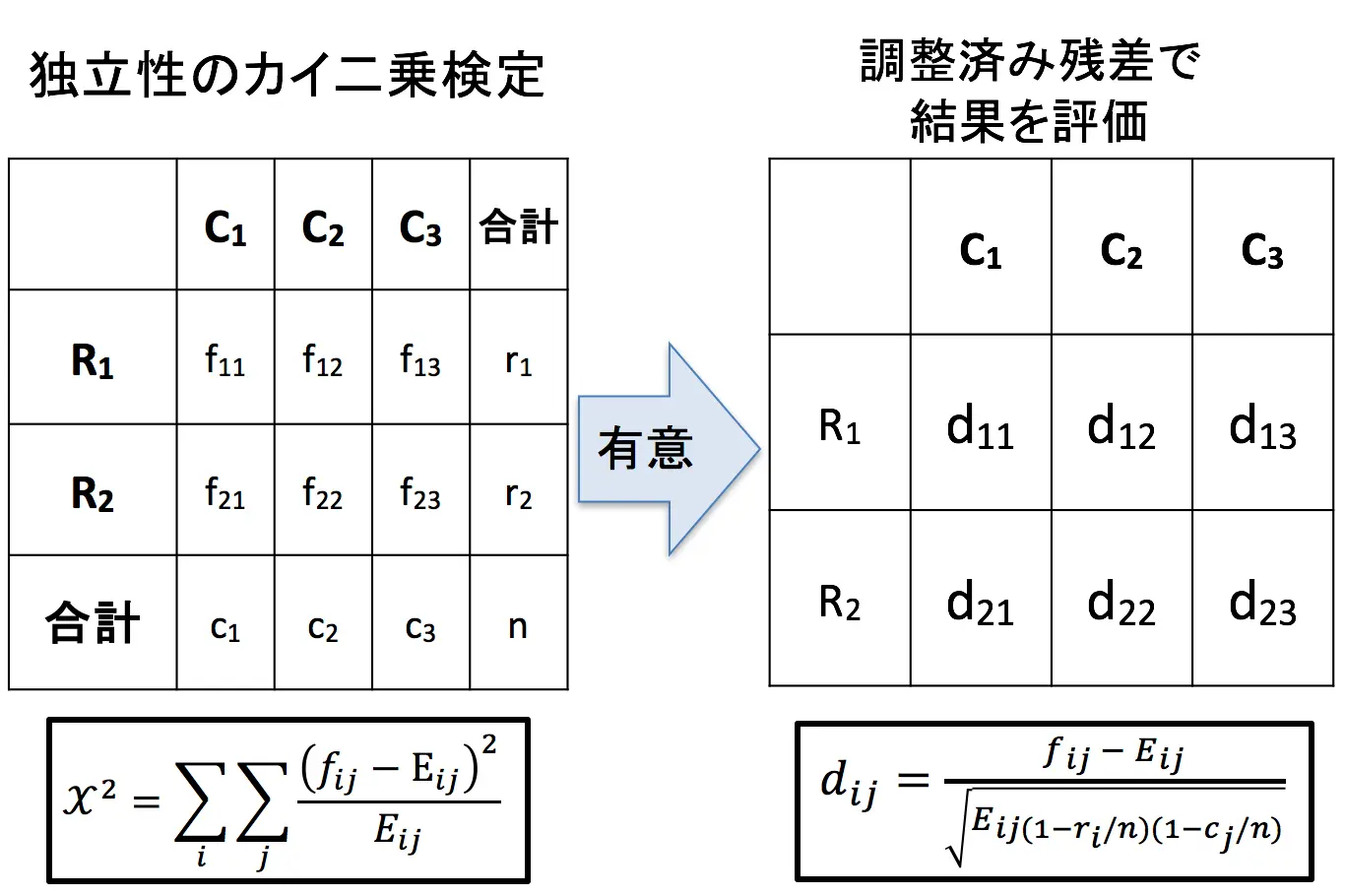
調整済み残差$d_{ij}$は標準正規分布に従うので、$|d_{ij}|≧1.96$のとき、そのセルを特徴的な部分であると考えることができます。

残差分析の例題

具体的な例で考えてみましょう。

130人に対してアンケートを実施し、体脂肪率と自分に自信があるかの調査を行い、以下の分割表のようになりました。

有意水準5%で独立性のカイ二乗検定を行い、有意だった場合には、調整済み残差を求めて特徴的なセルを見つけましょう。

ここで独立性のカイ二乗検定を行うとp値は0.02です。よって独立ではないという結論が得られたので調査済み残座を算出します。

$d_{ij} = \frac{f_{ij} - E_{ij}}{\sqrt{E_{ij}(1-r_i/n_i)(1-c_i/n_i)}}$

残差分析を行うと、以下のようになります。

上記から、体脂肪率が低い人に自信がある人が多く、体脂肪率が高い人に自信がない人が多いことが読み取れます。

標準の体脂肪率の人は正の方向・負の方向ともに1.96以上になっていないので特に特徴はありません。

調整済み残差の導出

調整済み残差$d_{ij}$は期待度数$E_{ij}$、周辺度数$r_i$、$n_i$と観測値$f_{ij}$を用いて、次のように表されます。

$d_{ij} = \frac{f_{ij} - E_{ij}}{\sqrt{E_{ij}(1-r_i/n_i)(1-c_i/n_i)}}$

ここから、上式の導出を説明します。

まず、独立性のカイ二乗検定を行って、独立ではないという結論が得られたとします。

ここで調整済み残差を求めたいのですが、調整済み残差を求める前の段階として標準化残差を求める必要があります。

残差とは「観測値$-$期待値」であり、それを標準偏差で割ったものが標準化残差です。

$e_{ij} = \frac{n_{ij}-E_{ij}}{\sqrt{E_ij}}$

標準化残差は、近似的に正規分布$N(0,v_{ij})$に従うことが知られており。その分散は次の式で表されます。

$v_{ij} = (1-\frac{n_{i.}}{N})(1-\frac{n_{.j}}{N})$

調整済み残差は、標準化残差とその分散を用いて標準化変換を行うことによって次の式で表されます。

$d_{ij} = \frac{e_{ij}}{\sqrt{v_{ij}}}$

したがって調整済み残差の分布は、近似的に平均0,標準偏差1の標準正規分布に従います。

よって、有意水準α=0.05の検定の場合は$|d_{ij}|$が1.96以上であれば、特徴的な部分であるとみなすことができます。

関連記事

独立性のカイ二乗検定を例題を用いてわかりやすく解説