ベイズ統計の区間推定を解説

頻度論とベイズ論の区間推定の違い

頻度論とベイズ論の区間推定について解説します。

頻度論における区間推定の考え方

頻度論における区間推定の考え方について説明します。

母分散既知の正規分布に従う標本からデータをn個取ってきたとき、母平均に関する区間推定は、有意水準を$\alpha$とすると、

$\bar{X}-Z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}\leq\mu\leq\bar{X}+Z_{\frac{\alpha}{2}}\sqrt{\frac{\sigma^2}{n}}$

と表せられます。このような区間は信頼区間と呼ばれています。

頻度論はパラメータを定数、データを確率変数として考えるので、上記の式を書き直すと、

$変数\leq定数\leq変数$

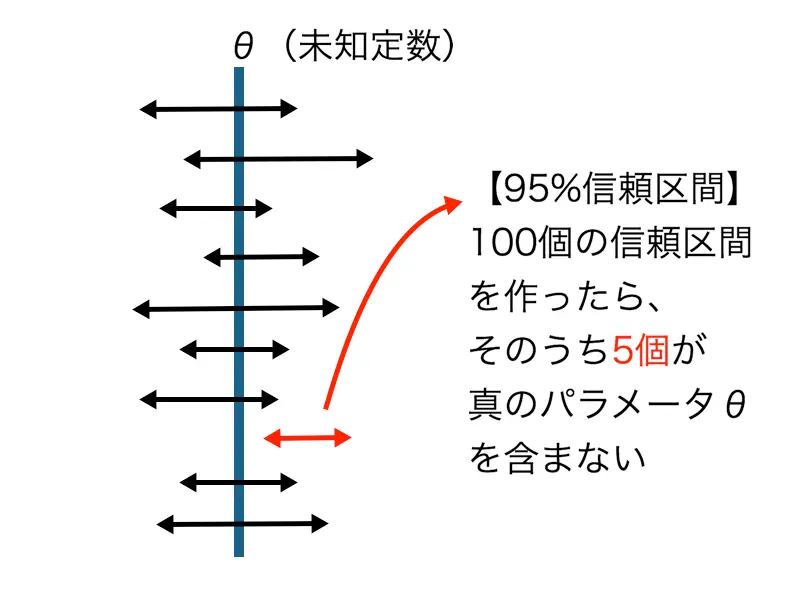
となり、区間が変数となることがわかります。つまり、得られるデータによって区間が変動するのです。

よって、95%信頼区間は「データを得て100個の信頼区間を作ったとき、95個の信頼区間が真のパラメータを含む」と解釈されます。

ベイズ論における区間推定の考え方

ベイズ統計ではパラメータを確率変数、データを定数として考えるので、上記の式は、

$定数\leq変数\leq定数$

と書き換えられ、区間が定数となります。

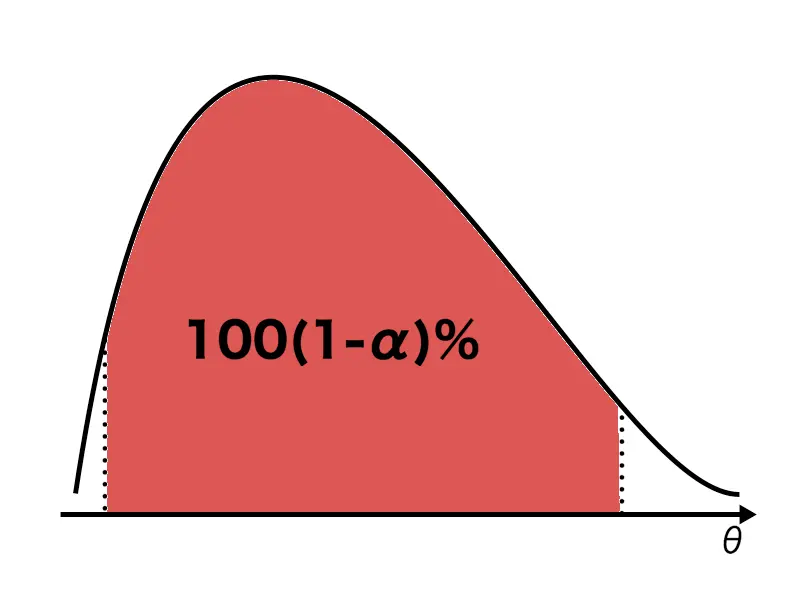
つまりベイズ統計の区間推定では、真のパラメータがその区間に存在する確率そのものが得られます。このような区間は信用区間（確信区間）と呼ばれています。

確率変数$\theta$の分布は事後分布によって与えられているので、$100(1-\alpha)$%信用区間は以下のように与えられます。

信頼区間と信用区間の違い

信頼区間と信用区間の違いを例題を通して解説します。

【例題】

日本人男性全体の平均身長$\mu$を調べたい。日本人男性全員を調査することは不可能なので、無作為に標本抽出をした。このデータから日本人男性全体の身長を推測したい。

⑴得られた標本から作成された95%信頼区間が$160\leq\mu\leq180$であった。この解釈を述べよ。
⑵得られた標本から作成された95%信用区間が$160\leq\mu\leq180$であった。この解釈を述べよ。

⑴今回作成された$160\leq\mu\leq180$という区間内に真の平均身長$\mu$を含む確率は95%である。「真の平均身長が165cm〜175cmである確率」などは存在せず、あくまでもこの区間内に真値を含むか否かでしか測れない。

⑵真の平均身長$\mu$を確率変数とみなす。このとき、確率変数$\mu$が$160\leq\mu\leq180$の値をとる確率が95%である。「真の平均身長が165cm〜175cmである確率」などが存在する。得られたデータから、真の平均身長をとる値を確率的に推測できる。

信用区間（確信区間）の定義

信用区間の定義は以下のようになります。

$\theta$の$100(1-\alpha)\%$区間とは、

$P\{C|X=x\}=1-\alpha$

を満たすような部分集合$C\subset\Theta$である。

ただし、$\theta$は連続型の確率変数

信用区間の種類

ベイズ統計の信用区間は、等裾事後信用区間と最高事後密度信用区間（HPD区間）の２つが有名です。

以下、$\alpha=\alpha_1+\alpha_2$、$\theta^{(1)}$、$\theta^{(2)}$をそれぞれ$100\alpha_1\%$点、$100\alpha_2\%$点として説明していきます。

等裾事後信用区間

$\alpha_1=\alpha_2=\frac{\alpha}{2}$と言うように$\alpha_1$、$\alpha_2$を選んだとき、得られる信用区間を等裾事後信用区間と言います。$95\%$等裾事後信用区間は以下のようになります。つまり、等裾事後信用区間は両裾を等しく切り捨てるような形になります。

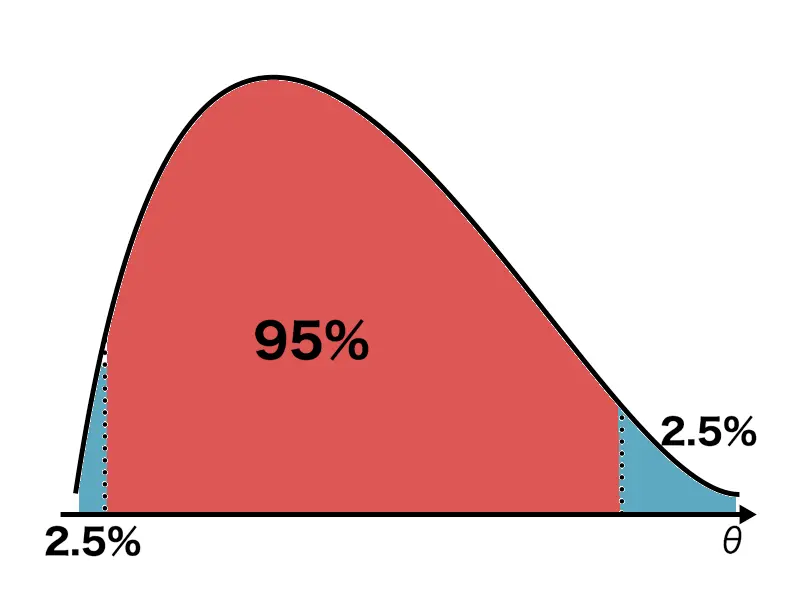
等裾事後信用区間には「信用区間を考えたとき、最頻値を必ずしも含まない」という問題点があります。

指数分布を例に考えて見ましょう。指数分布における等裾事後信用区間は以下のようになります。

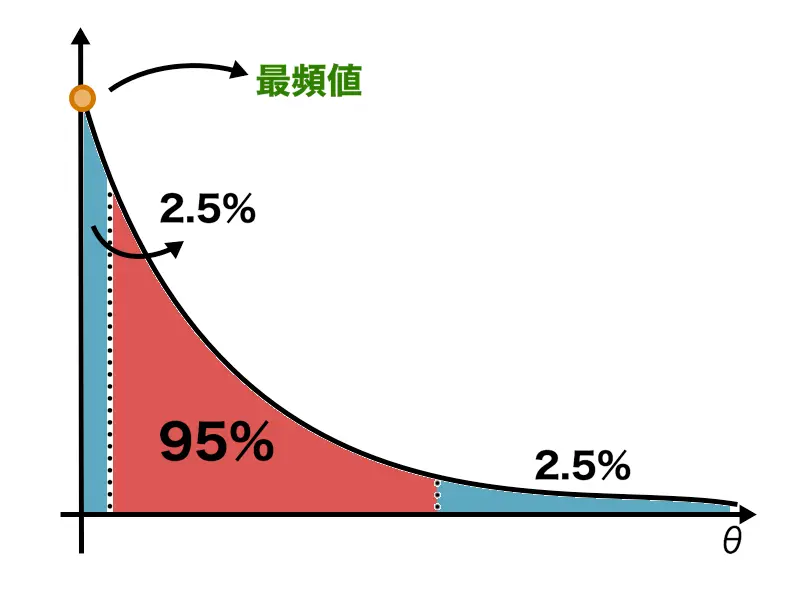
最も取りうる確率が高い（信用度の高い）$\theta=0$の部分が信用区間に入っていません。これを信用区間に採用するのは議論の余地がありそうです。

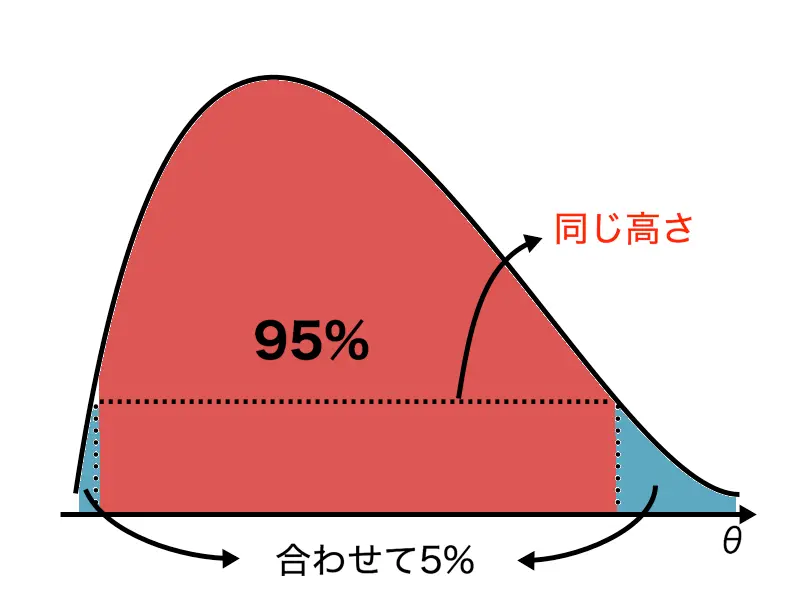
そこで、この問題を打開した最高事後密度信用区間（HPD区間）というものが現れました。

最高事後密度信用区間（HPD区間）

最高事後密度信用区間（HPD区間）は以下のように定義されます。

$C=\{\theta;\pi(\theta|X=x)\geq k\}$

を満たすような集合$C$を最高事後密度信用区間（HPD区間）という。ただし、$k$は

$P(C|X=x)=1-\alpha$

となるように選ばれる。

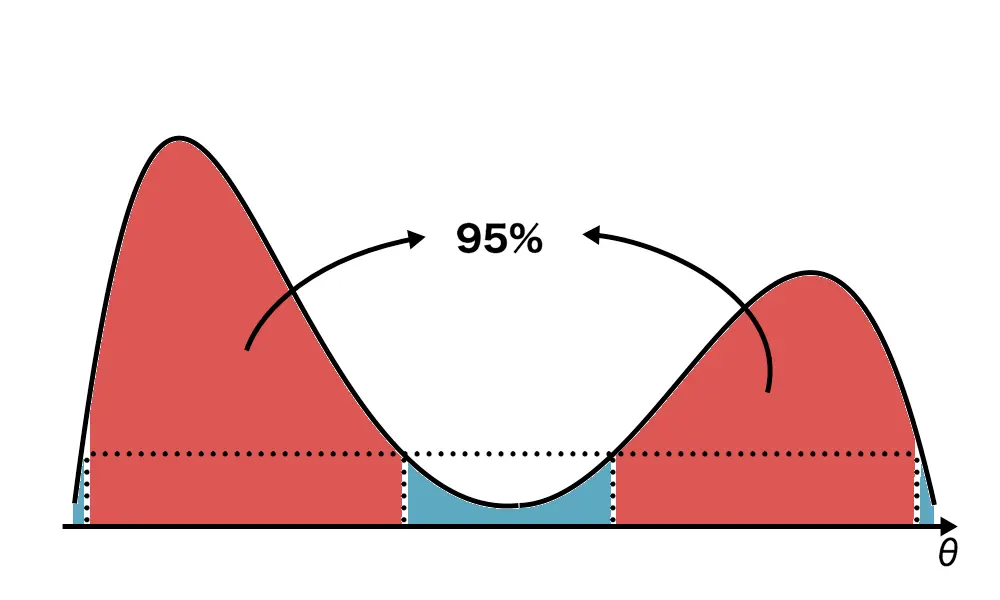
以下の画像のように、$\alpha_1+\alpha_2=\alpha$になるように$k$の高さを調整するイメージです。

 た、事後分布が単峰型でなくても扱うことができます。